【印刷可能】 y=(x-h)^2 k parabola 256053

Answer (1 of 6) Both points of xintercept satisfy the given equation y = (x h)^2 k, therefore (1,0) 0 = (1 h)^2 k —> k h^2 2h 1 = 0 (1) (8,0Y = (x h) 2 k So, if h = 3 and k = 4, we say that the reference parabola is horizontally translated 3 units and vertically translated 5 units Our equation for this would appear y = (x 3) 2 4 Here's the graph for these translations The reference parabola ( y = x 2) is drawn in transparent light gray, and the transformed parabola which is horizontally translated 3 units and Learn how to graph a parabola in the form y=(xh)^2k!Make sure to like this video if you found it helpful and feel free to leave feedback in the comments se

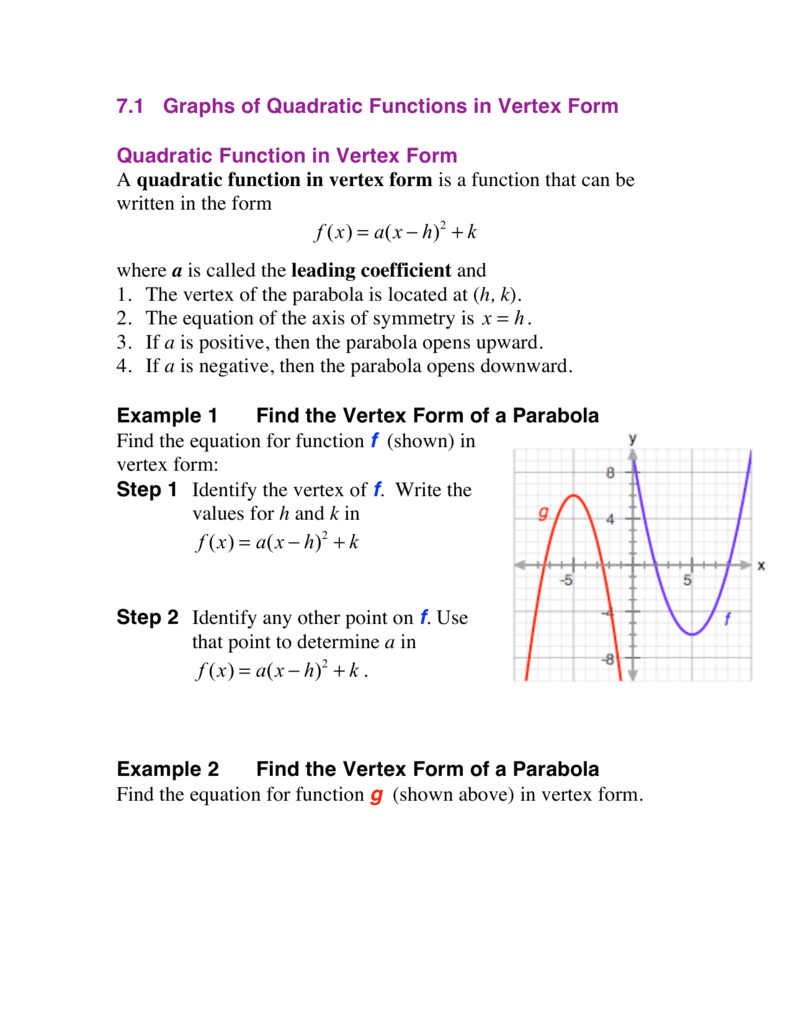
F X A X H 2 K F X A X H 2 K F X A X H 2 K

Y=(x-h)^2 k parabola

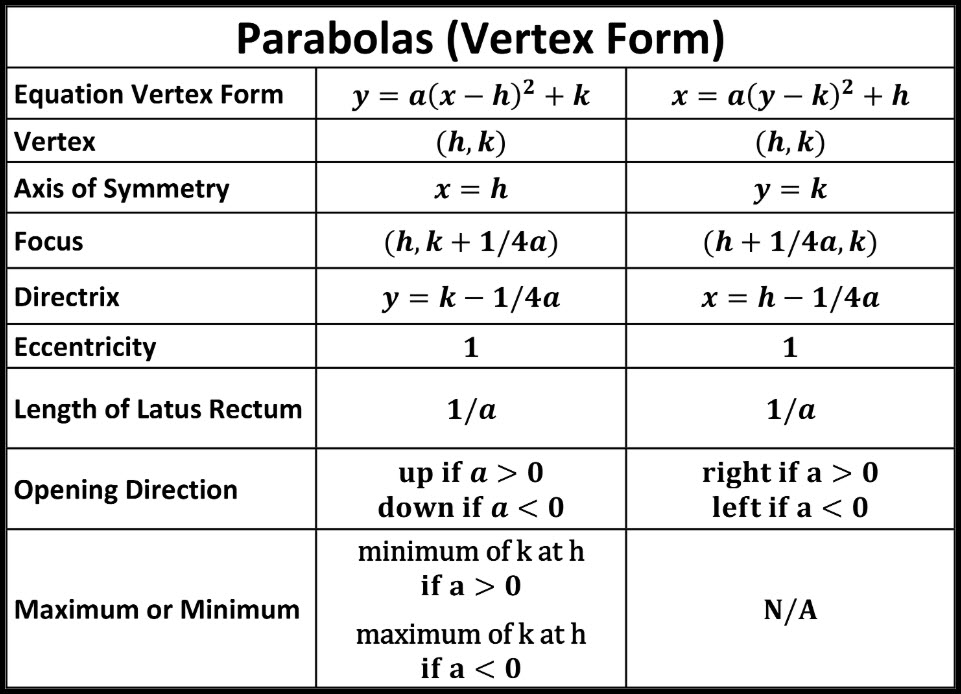
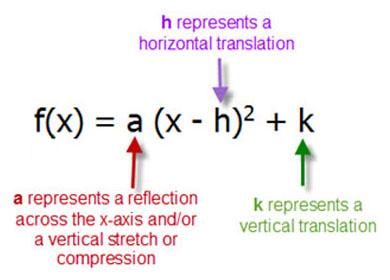
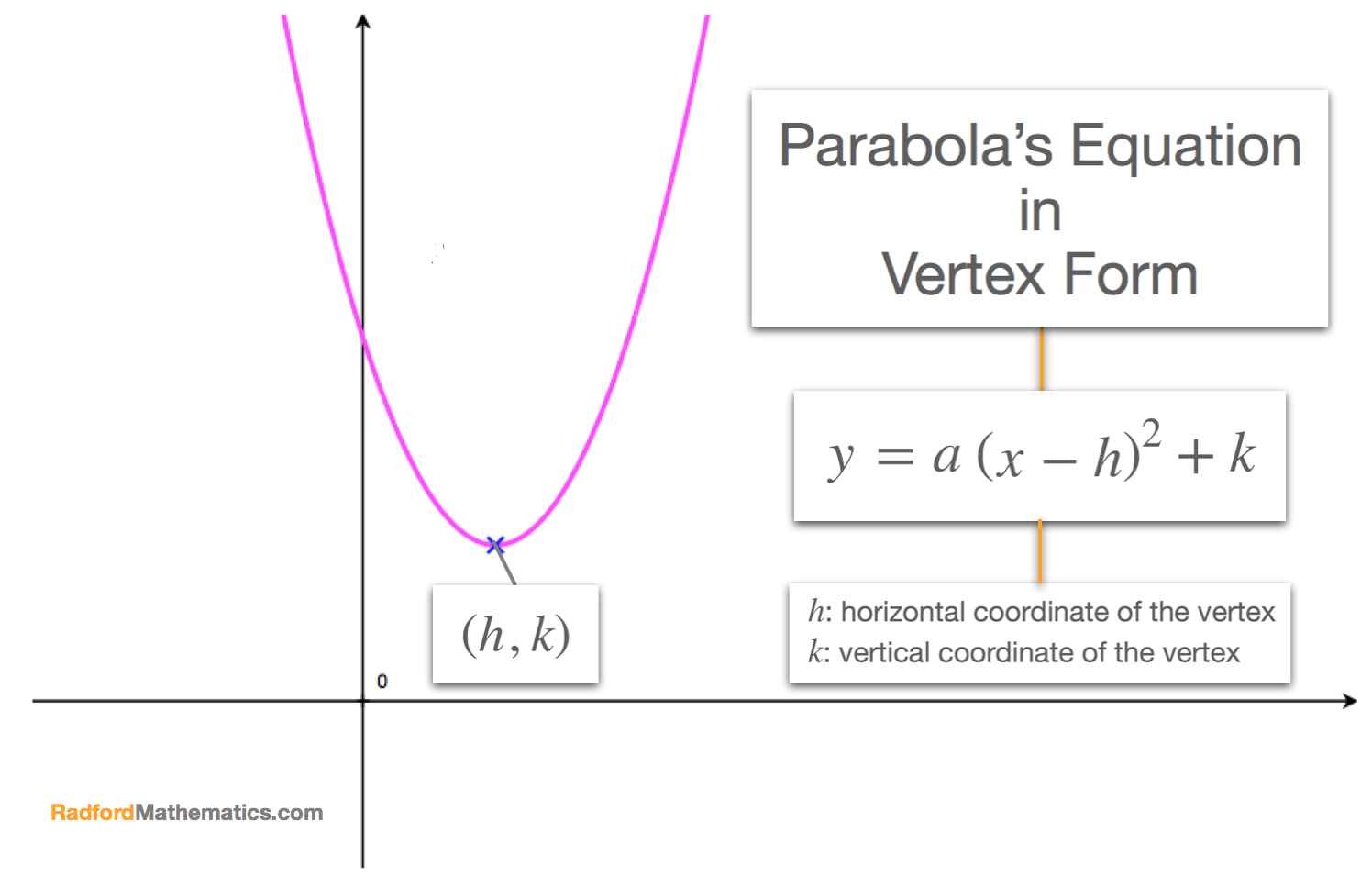
Y=(x-h)^2 k parabola-The vertex form of a parabola's equation is generally expressed as y = a(xh) 2 k (h,k) is the vertex as you can see in the picture below If a is positive then the parabola opens upwards like aFor horizontal parabolas, the vertex is x = a(y k) 2 h, where (h,k) is the vertex The focus of parabolas in this form have a focus located at (h , k) and a directrix at x = h The axis of symmetry is located at y = k Vertex form of a parabola The vertex form of a parabola is another form of the quadratic function f(x) = ax 2 bx c The vertex form of a parabola is f(x) = a(x

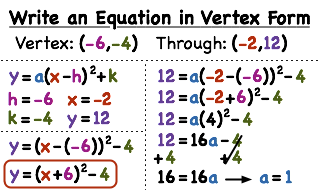
How Do You Write A Quadratic Equation In Vertex Form If You Have The Vertex And Another Point Printable Summary Virtual Nerd

En esta ecuación, el vértice de la parábola es el punto ( h , k ) Puede ver como se relaciona esto con la ecuación estándar al multiplicar y = a ( x – h ) ( x – h ) k y = ax 2 – 2 ahx ah 2 k El coeficiente de x aquí es – 2 ah Esto significa que en la forma estándar, y = ax 2 bx c , la expresión da la coordenadaThe general equation of a parabola is y = a(xh) 2 k or x = a(yk) 2 h, where (h,k) denotes the vertex The standard equation of a regular parabola is y 2 = 4ax Some of the important terms below are helpful to understand the features and parts of a parabola Focus The point (a, 0) is the focus of the parabola;Graph the parabola given by the equation {eq}y=(x2)^23 {/eq} Step 1 Comparing the equation to the general vertex form {eq}y=a(xh)^2k {/eq} of a

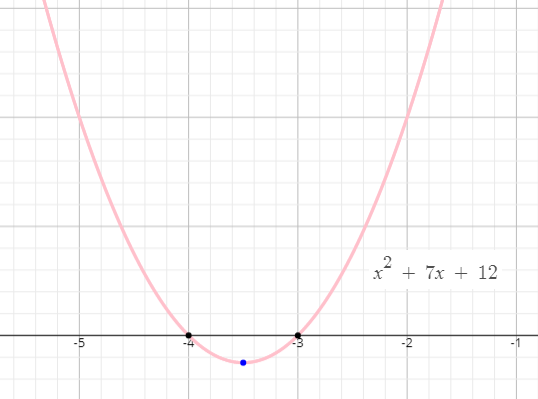
Axis Negative yaxis Thus, we can derive the equations of the parabolas as y 2 = 4ax y 2 = 4ax x 2 = 4ay x 2 = 4ay These four equations are called standard equations of parabolas It is important to note that the standard equations of parabolas focus on one of the coordinate axes, the vertex at the origin Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeNow the equation of the parabola is written in the form y = a(x h)^2 k, and this rewritten equation shows that the axis of the parabola is the vertical line x=1/3 and that the vertex is (1/3,4/3) Use these results, together with the intercepts and additional ordered pairs as needed, to get the graph in Figure 322 From the graph, the domain of the relation is

(y 4) 2 = (x 3) is in the form of (y k) 2 = 4a(x h) So, the parabola opens up and symmetric about xaxis with vertex at (h, k) = (3, 4) Comparing (y 4) 2 = (x 3) and (y k) 2 = 4a(x h), 4a = 1 Divide each side by 4 a = 1/4 = 025 Standard form equation of the given parabola (y 4) 2 = (x 3) Let Y = y 4 and X = x 3 Then, Y 2 = X Referred to X and Y Referred to xThe vertex form of a quadratic equation is y = m(xh)^2 k with m representing the slope of the line and h and k as any point on the line Standard Form To Vertex Form Factor Coefficient Factor the coefficient a from the first two terms of the standard form equation and place it outside of the parentheses Factoring standard form quadratic equations involves finding a pair of numbers thatPlotting the graph, when the quadratic equation is given in the form of f(x) = a(xh) 2 k, where (h, k) is the vertex of the parabola, is its vertex form Find all the parabola formulas for vertex, focus and directrix here In this article, we are going to learn how to graph a parabola in the standard form as well as in the vertex form with many solved examples Before plotting the parabola

Assignment 2 Investigating The Relationship Between The Two Standard Forms Of The Graph Of A Parabola

What Is Vertex Form Example Get Education

The line y=k1/4a represent in y=a(xh)^2k is Directrix Stepbystep explanation Directrix of a parabolaA directrix is a line which is perpendicular to the axis of symmetry of a parabola and it does not touch the parabola Also, for the standard equation of the parabola ieThe general equation of parabola is y = x² in which xsquared is a parabola Work up its side it becomes y² = x or mathematically expressed as y = √x Formula for Equation of a Parabola Taken as known the focus (h, k) and the directrix y = mxb, parabola equation is y − m x – b ² / ² m ² 1 = (x h)² (y k)² The vertex form of a parabola's equation is generally expressed as y = a(xh) 2 k (h,k) is the vertex as you can see in the picture below If a is positive then the parabola opens upwards like a regular "U" If a is negative, then the graph opens downwards like

The Standard Forms Of A Parabola

How To Find The Minimum Or Maximum Value Of A Function In Vertex Form

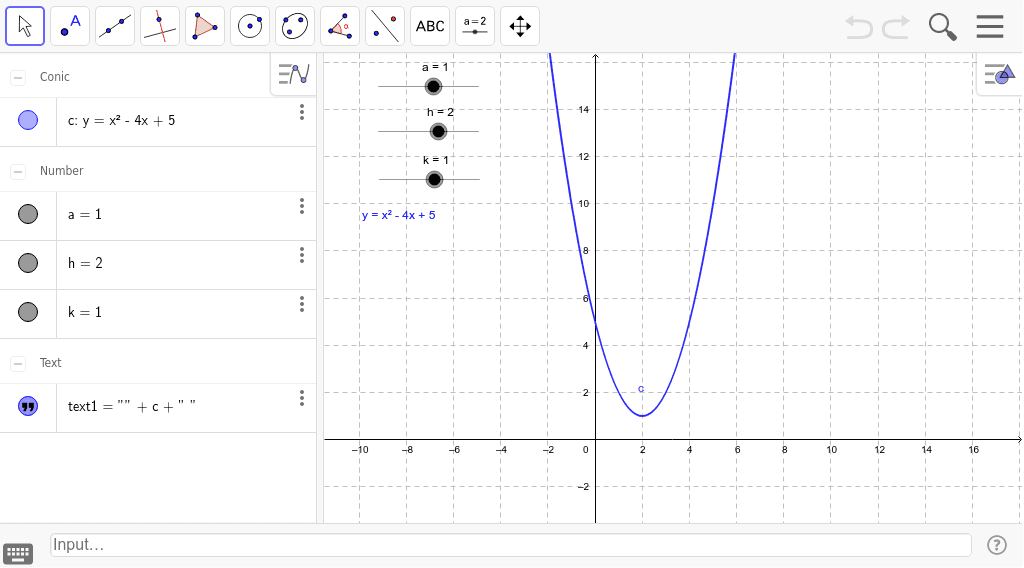
Smaller values of a expand it outwards;The vertex of a parabola is a specific point that represents the different values of the quadratic curve The vertex can be either maximum (when parabola going downward) or minimum (when parabola going up) Therefore, the vertex form is the intersection of a parabola with its symmetric axis Normally, the vertex is (h,The focus of this paper is to determine the characteristics of parabolas in the form y = a(x h) 2 k For our purposes, we will call this second form the shiftform equation of a parabola Given a quadratic in this form, it is fairly easy to predict the general shape of the parabola By examining a coefficient and the values for h and k, it is possible to determine the horizontal and

Illustrative Mathematics

Parabolas With Vertices Not At The Origin College Algebra

 We just have to put the values of h & k in the parabola equation Or in simple terms Substitute the vertex's coordinates for h and k in the vertex form For example, let the given vertex be (4, 5) Substituting 4 for h and 5 for k into y = a(x – h) 2Step 1 use the (known) coordinates of the vertex, ( h, k), to write the parabola 's equation in the form y = a ( x − h) 2 k the problem now only consists of having to find the value of the coefficient a Step 2 find the value of the coefficient a by substituting the coordinates of point P into the equation written in step 1 and solvingVertex Form (#y=a(xh)^2 k#) 1 Direction of the parabola can be determined by the value of a If a is positive, then the parabola faces up (making a u shaped) If a is negative, then the parabola faces down (upside down u) 2 Vertex is (h,k) Here is an example #y = 3(x2)6# Faces down since a = 3 and the vertex is (2, 6) Elizabeth P 2 How do you find the x

Quadratic Function Wikipedia

Quadratic Function

If the quadratic is written in the form y = a(x – h) 2 k, then the vertex is the point (h, k) This makes sense, if you think about it The squared part is always positive (for a rightsideup parabola), unless it's zero So you'll always have that fixed value k, and then you'll always be adding something to it to make y bigger, unless of course the squared part is zero So the smallest y Learn how to graph a parabola!Free Parabola calculator Calculate parabola foci, vertices, axis and directrix stepbystep This website uses cookies to ensure you get the best experience

Assignment 2 Investigating The Relationship Between The Two Standard Forms Of The Graph Of A Parabola

Quadratic Functions

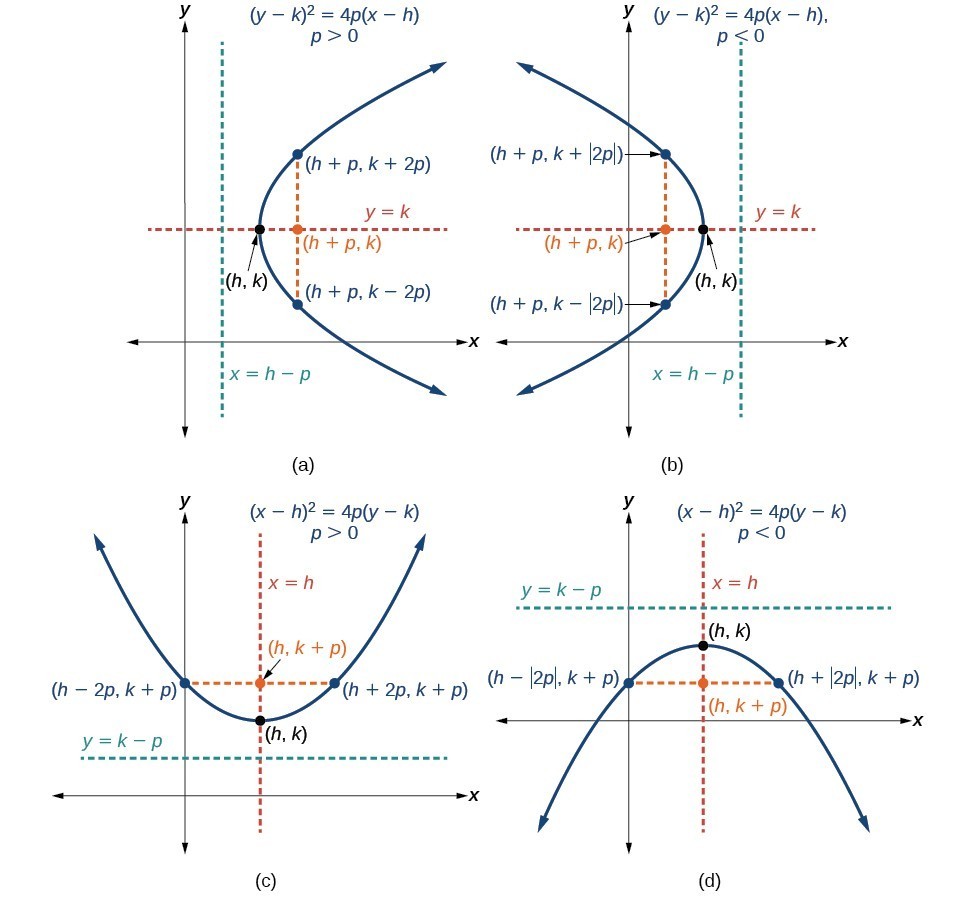
The standard form is (x h) 2 = 4p (y k), where the focus is (h, k p) and the directrix is y = k p If the parabola is rotated so that its vertex is (h,k) and its axis of symmetry is parallel to the xaxis, it has an equation of (y k) 2 = 4p (x h), where the focus is (h p, k) and the directrix is x = h p It would also be in our best interest to cover another form that theY = a x 2 b x c But the equation for a parabola can also be written in "vertex form" In this equation, the vertex of the parabola is the point ( h, k) You can see how this relates to the standard equation by multiplying it out y = a ( x − h) ( x − h) k y = a x 2 − 2 a h x a h 2 k This means that in the standard form, yDerive $y=a(xh)^2k$ from $y=ax^2bxc$ given a vertex and a point Recently I have been solving a problem to which I could not find a solution

Q 2 Connor Jennings

Parabolas Andymath Com

 The parabola defined by y = a(x h)² k has its vertex at (h,k) After a shift by h units right, followed by a shift of k units vertically, the parabola is defined by y = a(x 2h)² 2k which has its vertex at (2h, 2k) Answer The vertex gets shifted by h units horizontally and k units vertically Advertisement Advertisement Rascle123r Rascle123r ans is (h,k) just took testThe formula for the vertex form of a parabola is f(x) = a(x h) 2 k where a = vertical stretch or shrink of the parabola and (h, k) are the (x, y) coordinates of the vertex of the parabola h = the xcoordinate and k = the ycoordinate A Parabola is a Ushaped graph that is vertically symmetrical about a line that intersects the vertex of the graph A parabola can be rotated and faceDirectrix The line drawn parallel to the yaxis and passing through the

Vertex Form Introduction Video Khan Academy

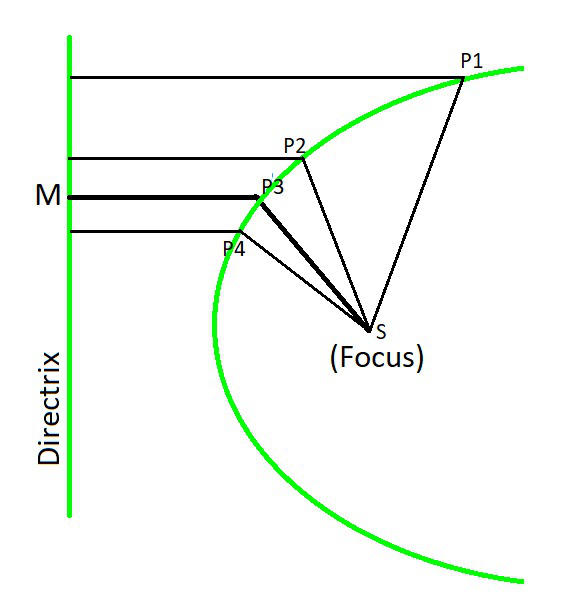
Focus And Directrix Of A Parabola Geeksforgeeks

A > 0, the parabola opens up and there is a minimum value a< 0, the parabola opens down and there is a maximum value (may also be referred to as a reflection in the xaxis) 1This is the curve f(x) = x 2 It is a parabola Now let us see what happens when we introduce the "a" value f(x) = ax 2 Larger values of a squash the curve inwards;Parabola equation in vertex form \( x = a(yk)^2 h \) Even the parabola calculator helps to turn the equation into the vertex form through which you can readily find the crucial points of the parabola How to Find the Equation of a Parabola?

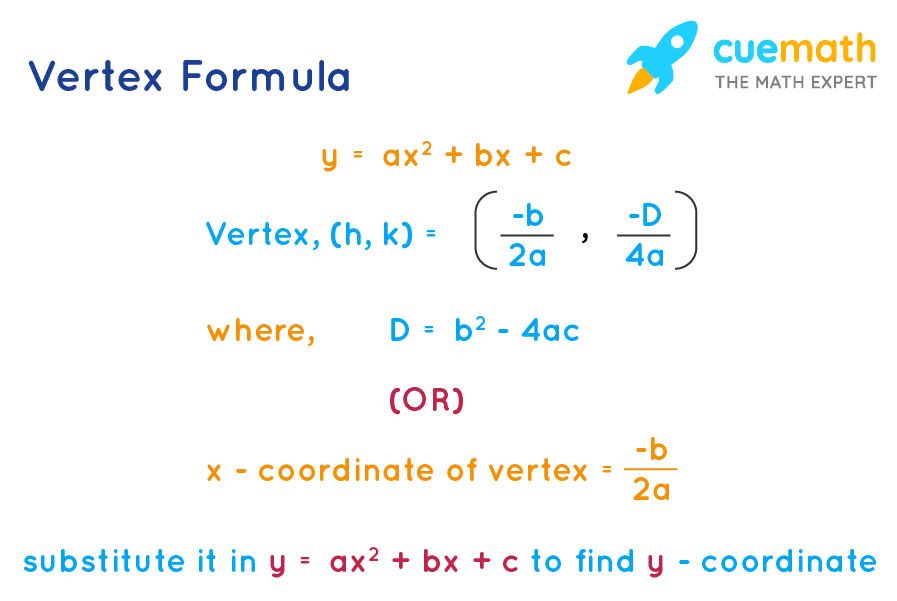
Vertex Formula What Is Vertex Formula Examples

Quadratic Functions

A vertex is the intersection point of the x and y coordinates of k(x h) 2 2yp 2pk = 2yp 2pk (x h) 2 = 4yp 4pk (x h) 2 = 4p(y k) The equation (x h) 2 = 4p(y k) above applies when the parabola opens upward or downward with a directrix of y = kp If the parabola opens to the right or to the left with a directrix of x = hp, the equation to use is (y k) 2 = 4p(x h) Now let us practice Suppose the parabola (y – k) 2 = 4 (x – h), with vertex A, passes through O = (0, 0) and L = (0, 2) Let D be an end point of the latus rectum Let the yaxis intersect the axis of the parabola at P Then ∠ PDA is equal to (A) tan –1 2/19 (B) tan –1 4/19 tan –1 4/19 (D) tan –1 8/19

Quadratic Equation Wikipedia

Ppt Example 1 Powerpoint Presentation Free Download Id

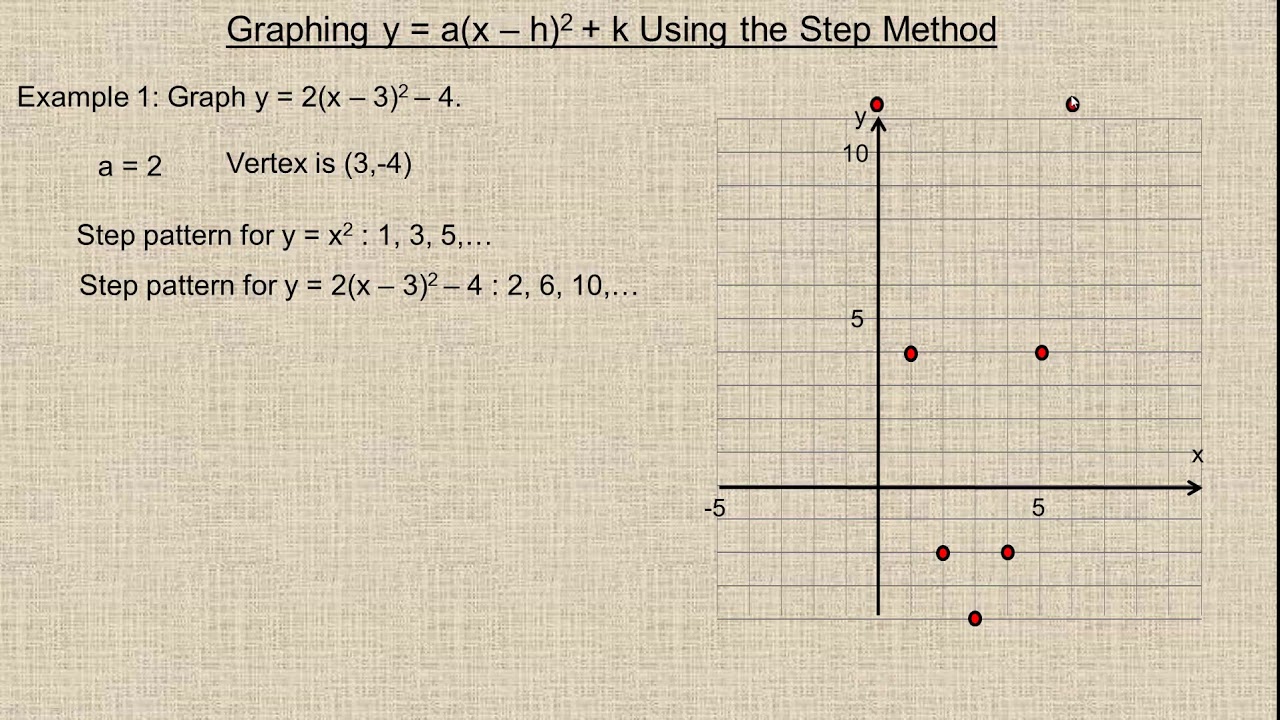
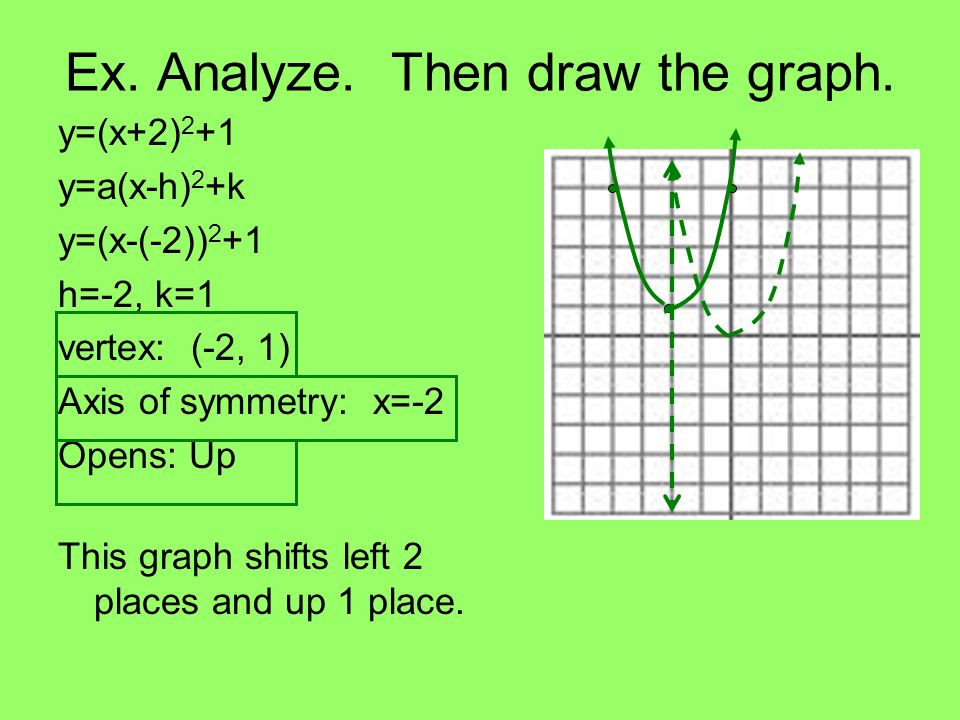
$$ y = a(x – h)^2 k $$ How to find the vertex of a parabola?Standard form of equation for a parabola y=A(xh)^2k, (h,k)=(x,y) coordinates of the vertex, A is a coefficient which affect the slope or steepness of the curve axis of symmetry, x=2, means the xcoordinate of the vertex=2 Using coordinates of given points,(0,1) and (2,5), to set up two equations with unknowns A and k 1=A(02)^2k 5=A(22)^2k 1=4Ak5=16Ak subtractGraphing y = (x h) 2 k In the graph of y = x 2, the point (0, 0) is called the vertex The vertex is the minimum point in a parabola that opens upward In a parabola that opens downward, the vertex is the maximum point We can graph a parabola with a different vertex Observe the graph of y = x 2 3 Graph of y = x 2 3 The graph is shifted up 3 units from the graph of y = x 2, and the

1

Consider The Parabola Graphed Below Is Of The Form Y X H 2 K Brainly Com

Parabola Equations Graphing Parabolas Students learn to graph quadratic equations that are written in y k = a(x h) 2 form by using the coordinates (h, k) to graph the vertex, and using the x and yintercepts to graph the parabola Students are reminded that to find the yintercept, they must substitute a 0 in for x, and to find the xintercept(s), they must substitute a zero in for yThe vertex form of the parabola y = a(x h) 2 k There are two ways in which we can determine the vertex(h, k) They are (h, k) = (b/2a, D/4a), where D(discriminant) = b 2 4ac (h,k), where h = b / 2a and evaluate y at h to find k Vertex Formula The two vertex formulas to find the vertex is Formula 1 (h, k) = (b/2a, D/4a) where, D is the denominator;Answer (1 of 5) Well, you have the equation of your parabola in the vertex form of y = a(x h)^2 k => where (h, k) is the coordinates of the vertex so in this case y = ax^2 k => the only information given is that the xcoordinate of your vertex(h) is zero thus you need to find a and k,

Practice 7 Fill In The Blanks The Vertex Form Of A Parabola Is Y A X H 2 K Where Is The Brainly Com

Vertex And Intercepts

And negative values of a flip it upside down Play With It Now is a good time to play with the "Quadratic Equation Explorer" so you can see what different values of a, b and c do The(x h)2 = 4p(y k) Directriz y= k p Y X V(h,k) 0 UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE INGENIERÍA DIVISIÓN DE CIENCIAS BÁSICAS COORDINACIÓN DE MATEMÁTICAS Abril De 11 7 de 8 Figura 9 Parábola con vértice en (h, k) y eje focal paralelo al eje Y con p < 0 Ejemplo Determinar las coordenadas del Vértice, Foco y calcular el lado rectoThe Parabola Algebraic Definition of The Parabola Recall that the standard equation of the parabola is given by y = a (x h) 2 k If we are given the equation of a parabola y = ax 2 bx c we can complete the square to get the parabola in standard form Geometry of the Parabola We can define a parabola as follows

2

Transformations Review Vertex Form Y A X H 2 K The Vertex Form Of A Quadratic Equation Allows You To Immediately Identify The Vertex Of A Parabola Ppt Download

Well, we can evaluate the axis of symmetry, focus, directrix, vertex, x intercept, y intercept by using the parabola formula in the form of \( xQuadratic functions The general equation of a quadratic function in vertex form is {eq}y=a(xh)^2k {/eq}, where {eq}h,k {/eq} are the coordinates of the center of the parabola and coefficientH,k are the coordinates of

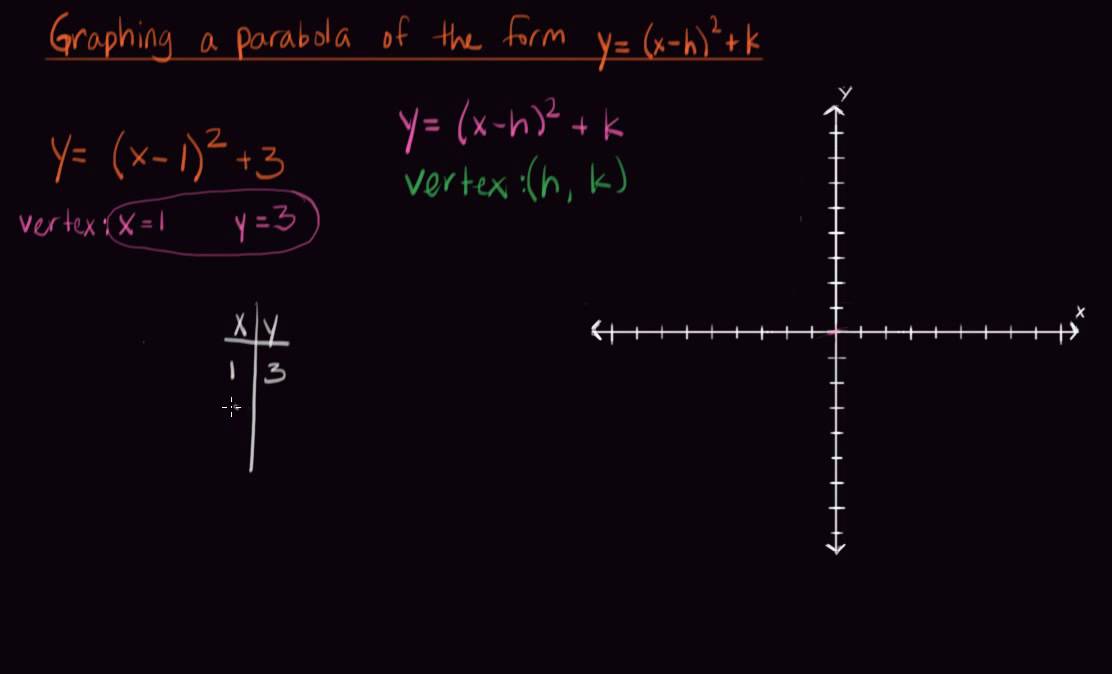
Graphing A Parabola Of The Form Y X H 2 K Youtube

Vertex Form Of Quadratic Equation Mathbitsnotebook A1 Ccss Math

What you need is that the system formed by the parabolas y^2=4ax and (yk)^2=4a(xh) had only one solution (at the point of tangency) If you solve for x in the first and substitute in If you solve for x in the first and substitute in

Graph Quadratic Functions

Parabolas Andymath Com

Solved Use The Equation Of The Parabola In Standard Form Y A X H 2 K To Determine The Coordinates Of The Vertex And The Equation Of The Axis Of Symmetry Complete The Square If Necessary Then Graph

Parabola Y A X H 2 K Geogebra

Forms Of Quadratics Explanations Tips And Examples Albert Resources

Section 5 3 Transforming Parabolas Standard Form Vs Vertex Form Standard Form Is Y Ax 2 Bx C Vertex Form Is Y A X H 2 K Ppt Download

Standard Form To Vertex Form Calculator Mikes Calculators With Steps Free 21

Graphing Y A X H K Using The Step Method Youtube

6 6 Analyzing Graphs Of Quadratic Functions Ppt Download

Untitled Document

F X A X H 2 K F X A X H 2 K F X A X H 2 K

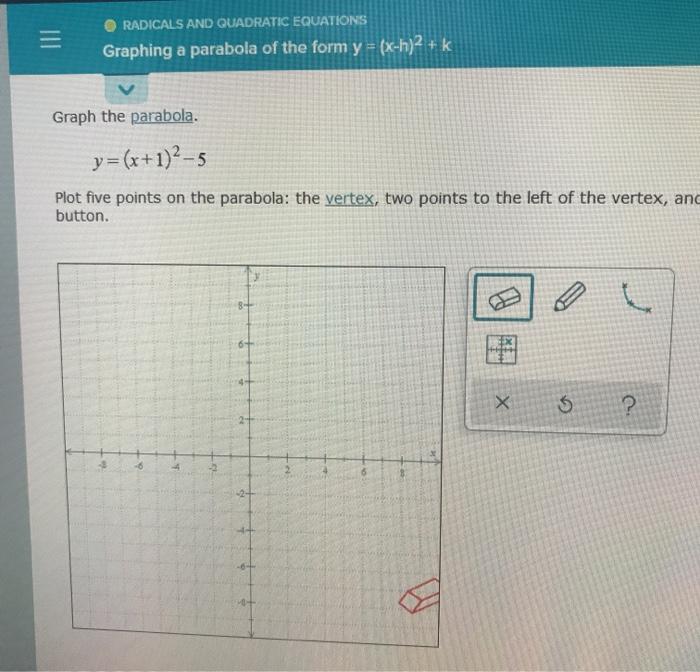
Solved Radicals And Quadratic Equations Graphing A Parabola Chegg Com

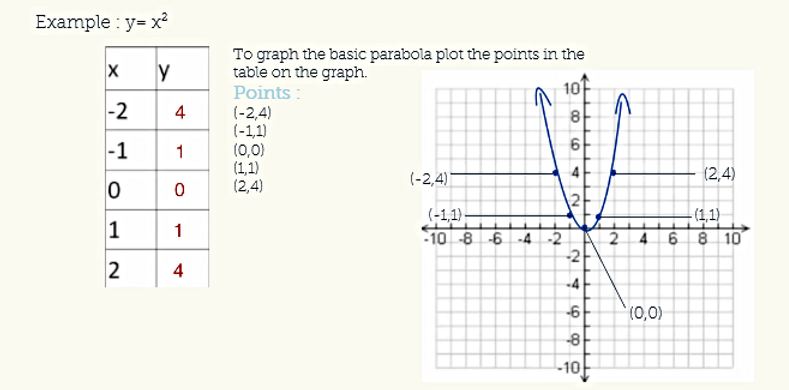
Vertex Form Quadratics

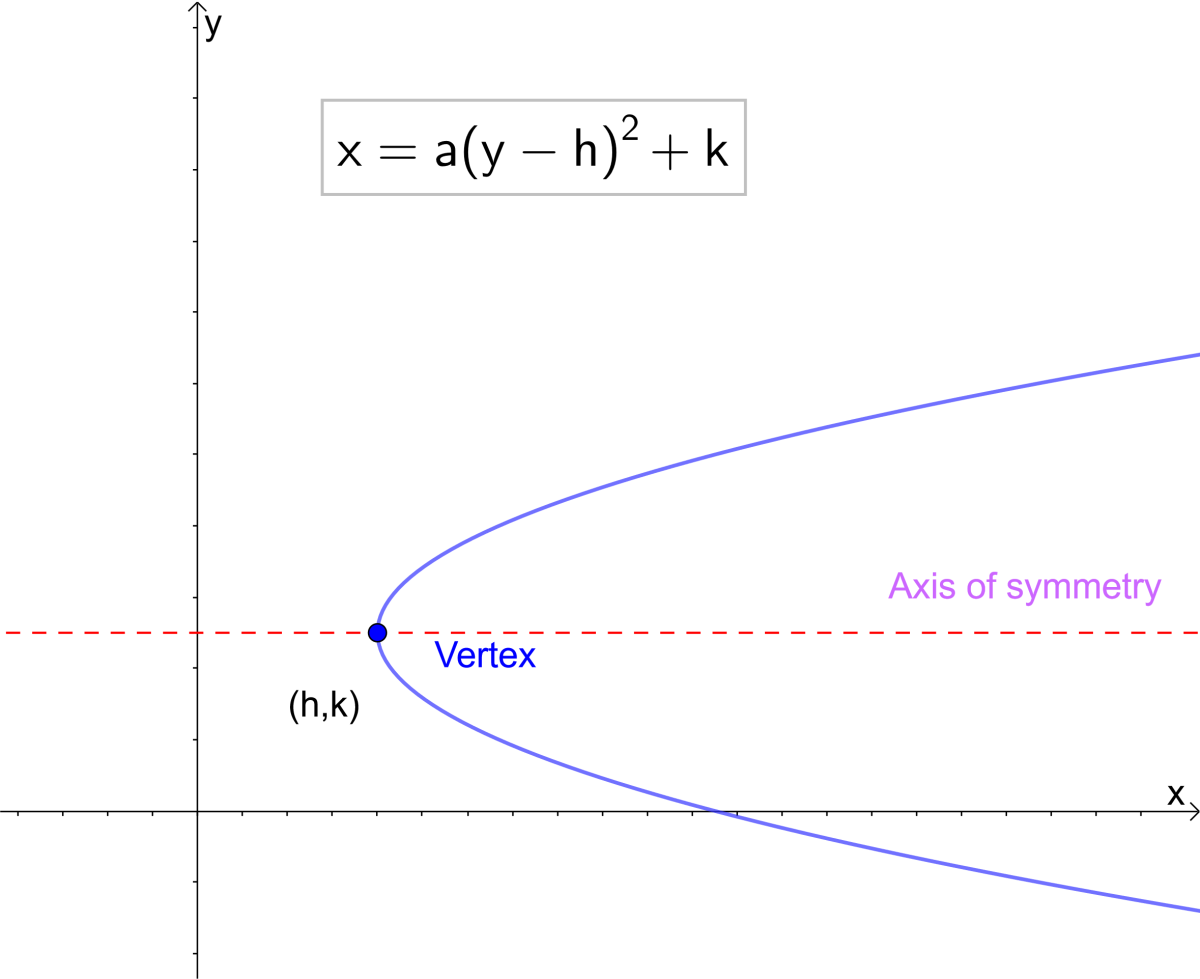
Parabola Equations And Graphs Directrix And Focus And How To Find Roots Of Quadratic Equations Owlcation

Quadratics Graphing Parabolas Sparknotes

Solution 1 Graph X 3 1 8 Y 2 2 Write The Coordinates Of The Vertex And The Focus And The Equation Of The Directrix 2 Find All Solution To Each System Of Equations Algerbaiclly

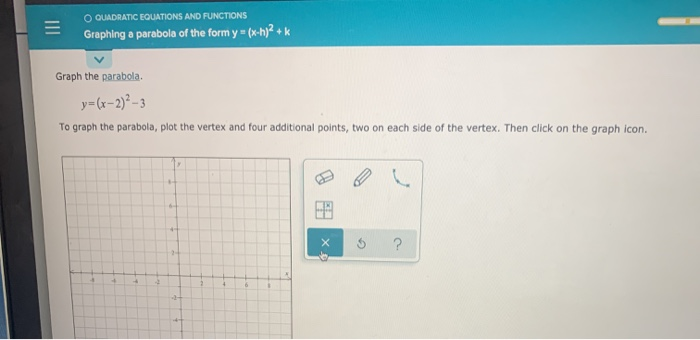
Solved O Quadratic Equations And Functions Graphing A Chegg Com

Conic Sections 11 1 Parabola Conic Sections Parabola

Standard And Vertex Form Of The Equation Of Parabola And How It Relates To A Parabola S Graph

Finding Features Of Quadratic Functions Video Khan Academy

Lesson 4 Parabolas In This Lesson Students Will Become Familiar With The Equations And Graphs Of Parabolas The Definition Of A Parabola Will Be Learned Both Algebraically And Using The Distance Relationship Students Will Learn How To Construct A Parabola

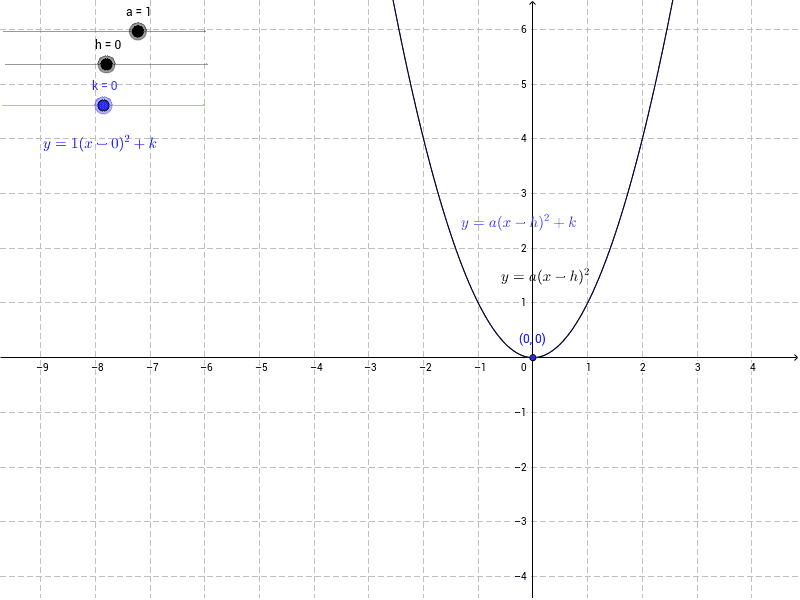
Investigating The Graph Of Y X H 2 K Geogebra

1

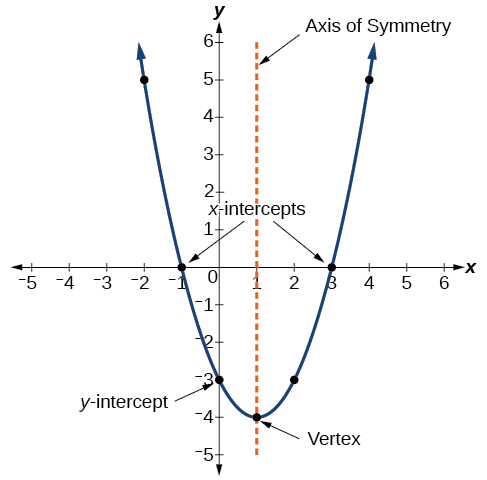
5 2 Quadratic Functions Mathematics Libretexts

Parabolas With Vertex At H K Ck 12 Foundation

Quadratic Equations Parabolas Flashcards Quizlet

Quick Review Before Hw Quiz Y A X H 2 K Form Vertex H K Axis X H Up If A 0 Down If A 0 Ex Y X 1 2 4 Y 1 X 1 2 4 A 1

In Vertex Form Y A X H 2 K Which Letter Indicates A Stretch Change In Width Quora

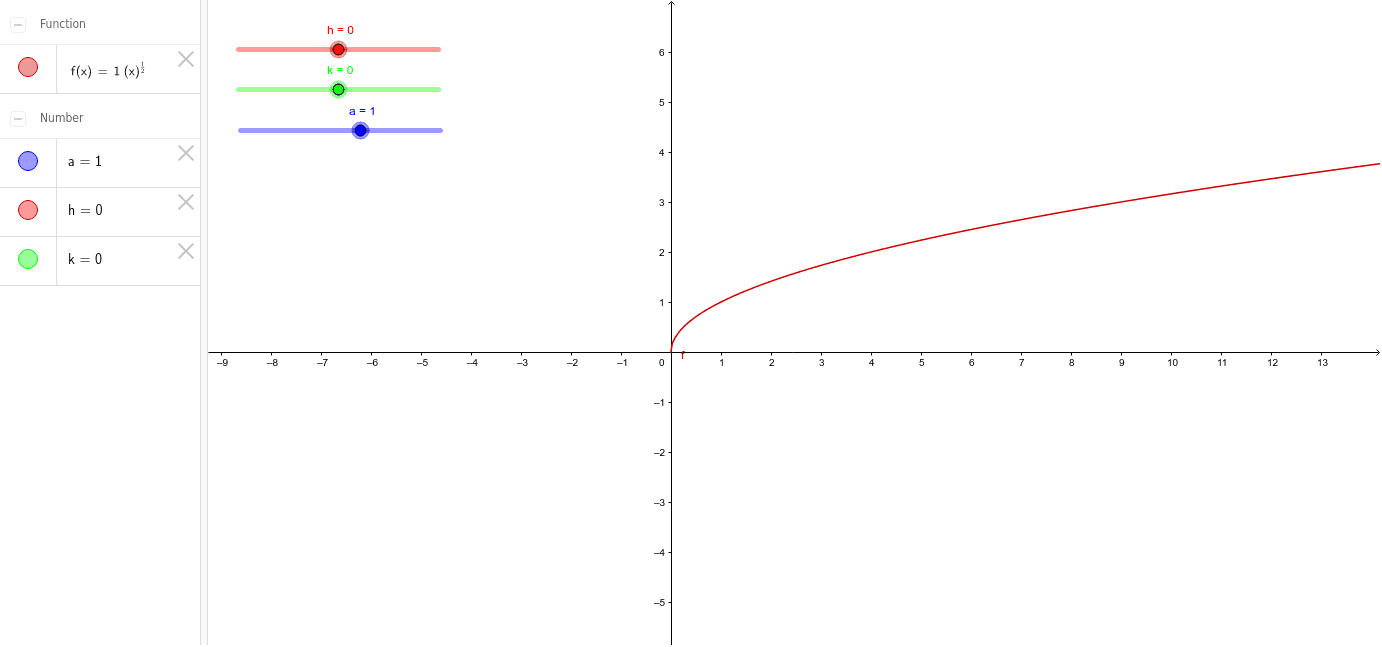
Y A X H 1 2 K Geogebra

What Is The Equation Of A Parabola Whose Axis Is Parallel To The X Axis As It Passes Through Points 4 2 2 1 And 7 2 1 Quora

Pslv Conic Section

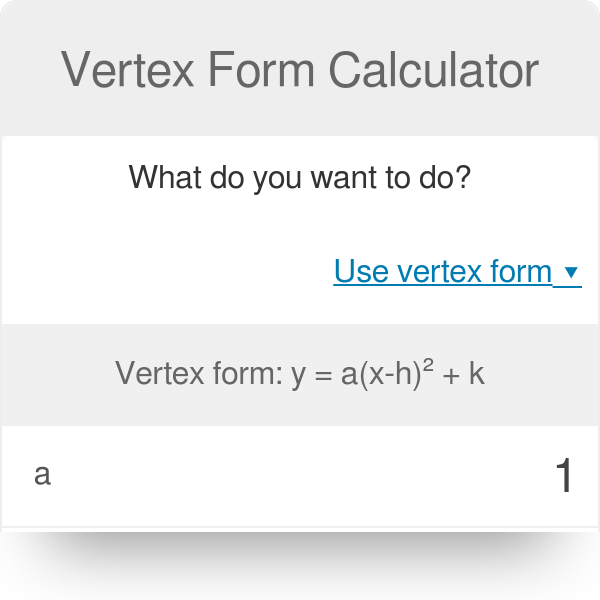
Vertex Form Calculator

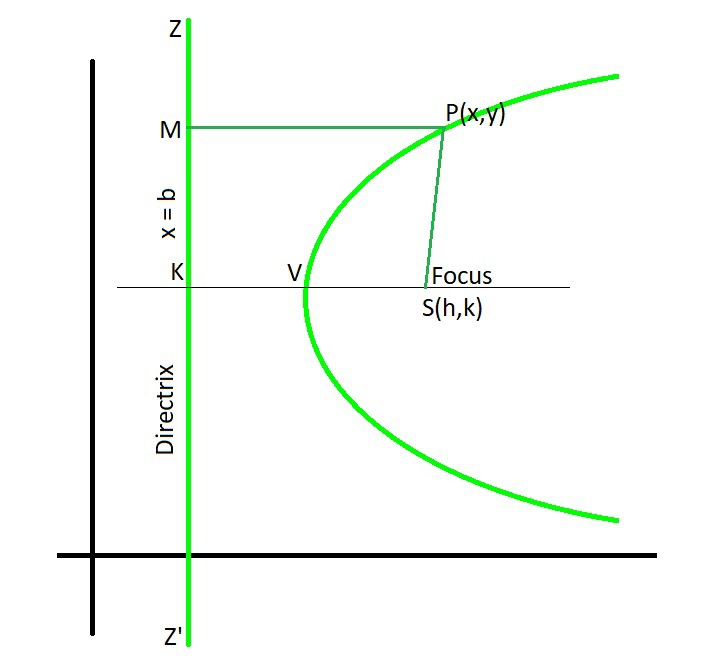
Focus And Directrix Of A Parabola Geeksforgeeks

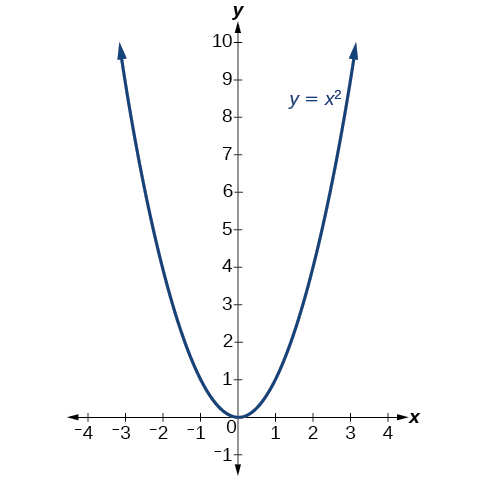
5 2 Quadratic Functions Mathematics Libretexts

How To Write An Equation For A Parabola In Vertex Form Wyzant Ask An Expert

Vertex Form

Quadratic Functions

Vertex Form Vertex Form Vertex Form Is Another

Ppt Quadratics Of The Form Y A X H 2 K Powerpoint Presentation Id

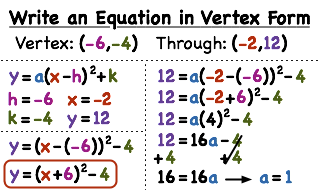
How Do You Write A Quadratic Equation In Vertex Form If You Have The Vertex And Another Point Printable Summary Virtual Nerd

Standard Form To Vertex Form Definitions Facts And Solved Examples Cuemath

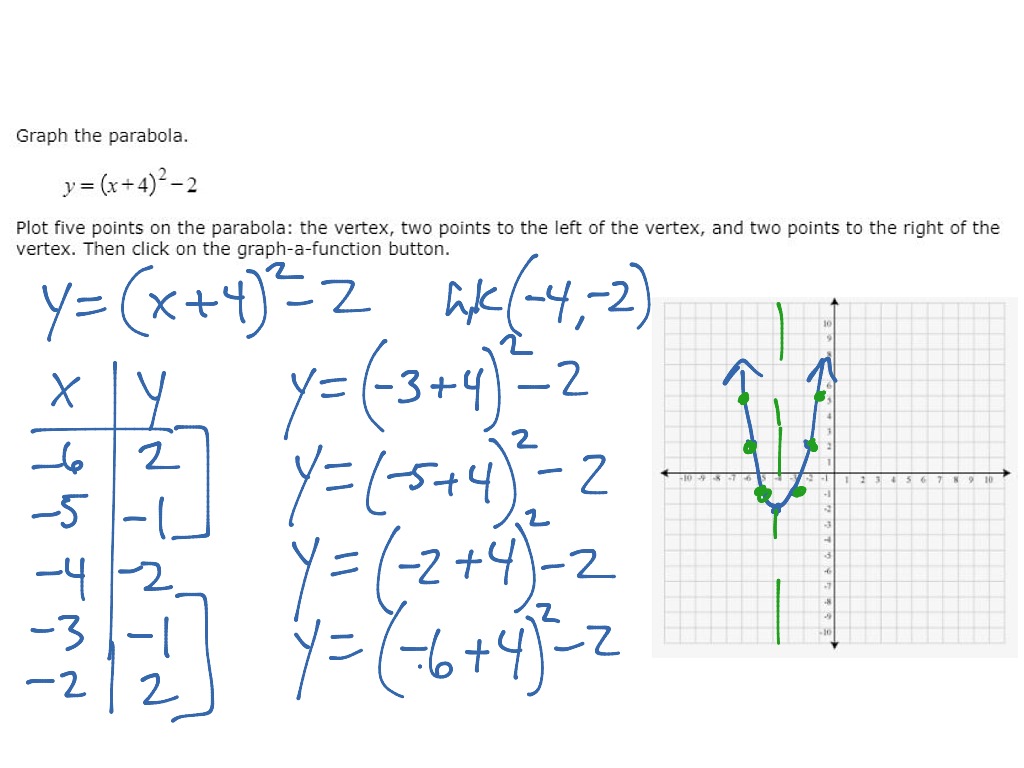
Math 1050 Graphing Parabola Y X H 2 K Math Showme

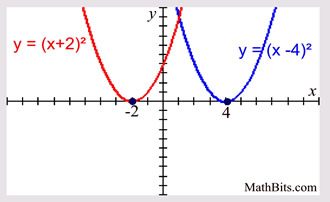
Parabola Parent Function Mathbitsnotebook A1 Ccss Math

Explaining A And H When You Have Y A X H 2 Youtube

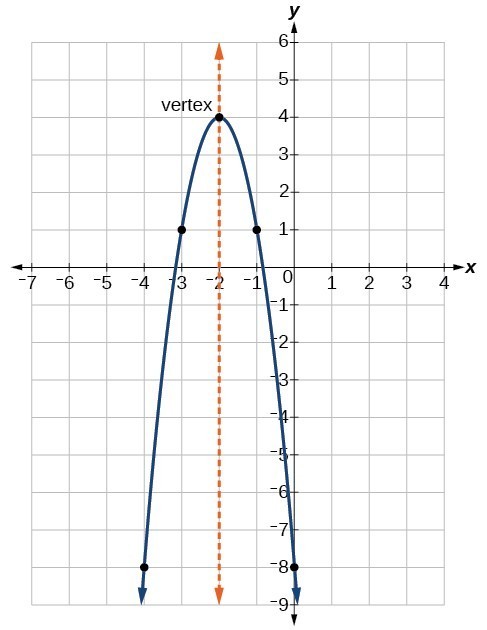
Understand How The Graph Of A Parabola Is Related To Its Quadratic Function College Algebra

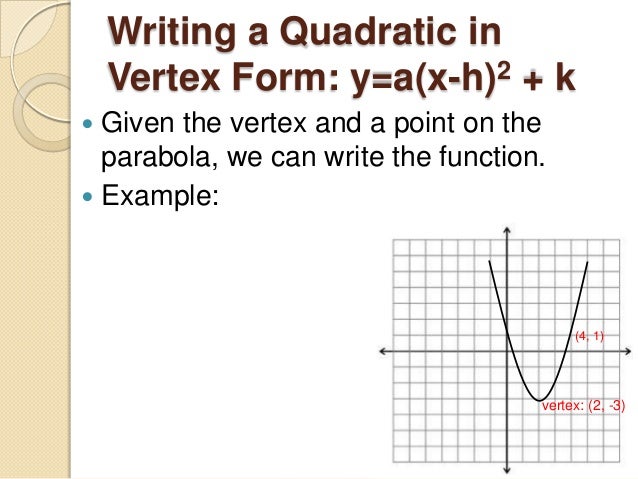
5 8 Modeling With Quadratic Functions

Ex Write Ax 2 Bx C In The Form A X H 2 K Negative A Youtube

Parabola Conic Section Warmup Graph The Following Parabola

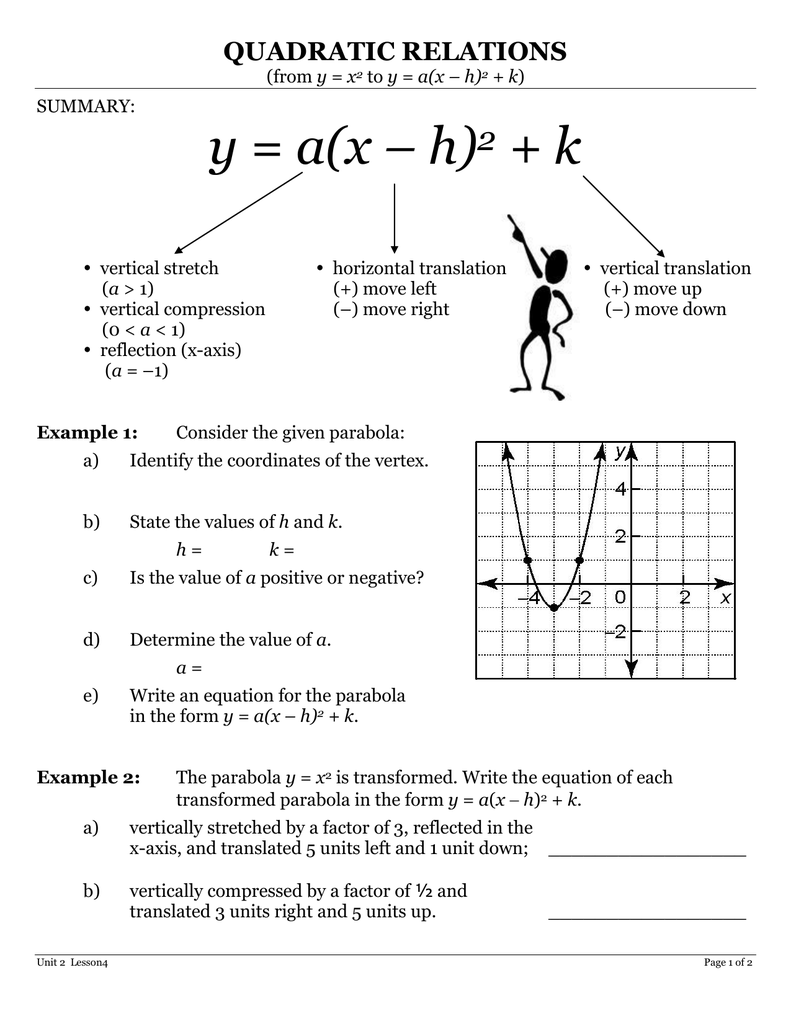
Y A X H K 2 Quadratic Relations

How To Graph A Parabola Of The Form Y A X H 2 K Algebra Study Com

Vertex Form Quadratics

Quadratic Formula Calculator

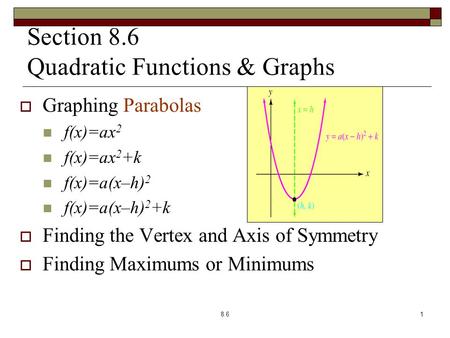
Transformations Review Vertex Form Y A X H 2 K The Vertex Form Of A Quadratic Equation Allows You To Immediately Identify The Vertex Of A Parabola Ppt Download

Vertex Form In 5 Minutes What Is Vertex Form How Do I Find It Mikes Calculators With Steps Free 21

1

Vertex Intercept And Standard Form Ck 12 Foundation

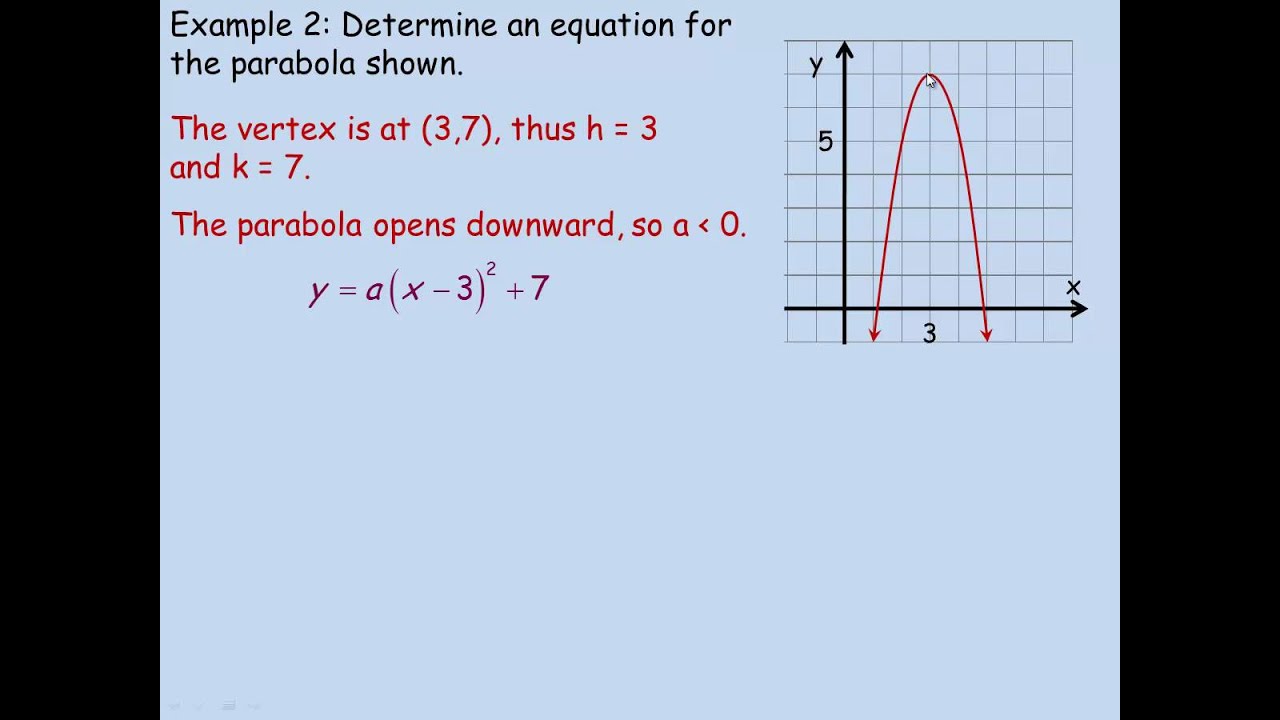
Graphing Y A X H K Youtube

Quadratic Function

How To Graph A Parabola Of The Form Y X H 2 K Algebra Study Com

Graphing A Parabola In The Form Y X H 2 K Youtube

Polynomial Functions Quadratic Functions Sparknotes

Unit 5 Quadratic Functions Flashcards Quizlet

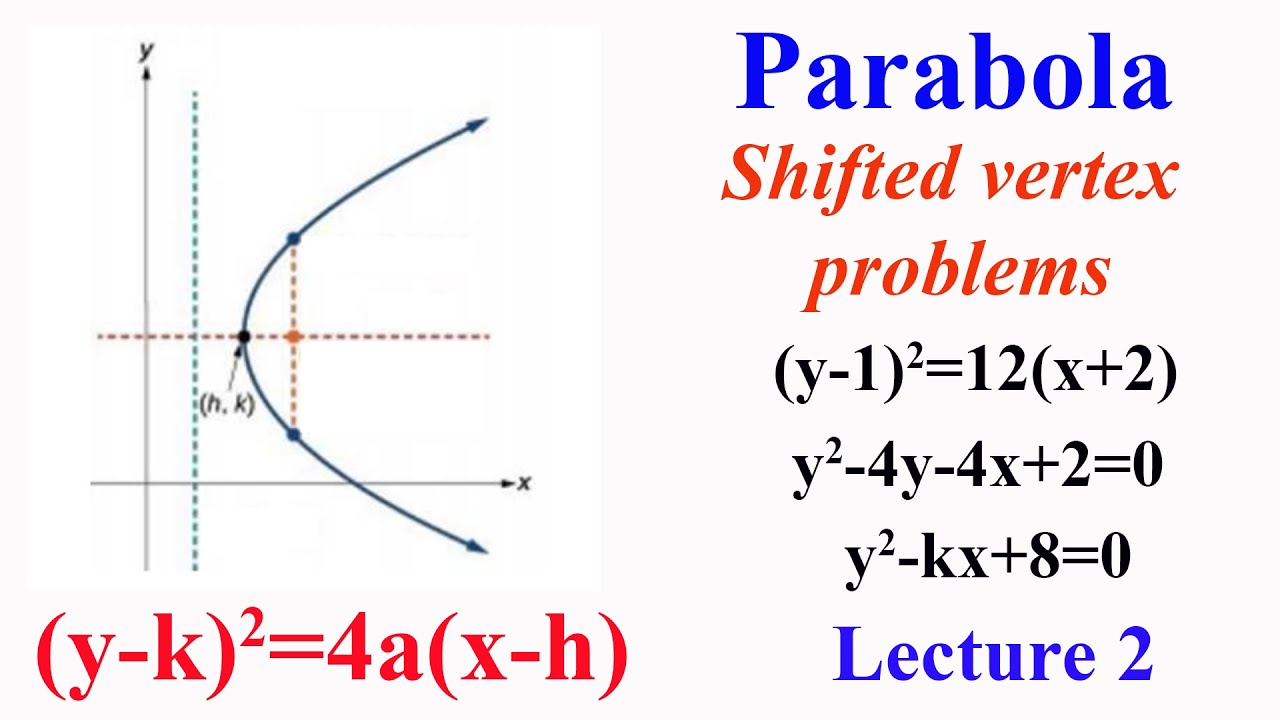
Parabola Lecture 2 Shifted Vertex Y K 2 4a X H With Examples Youtube

Quadratics Graphing Parabolas Sparknotes

Vertex Form Quirky Quadratics

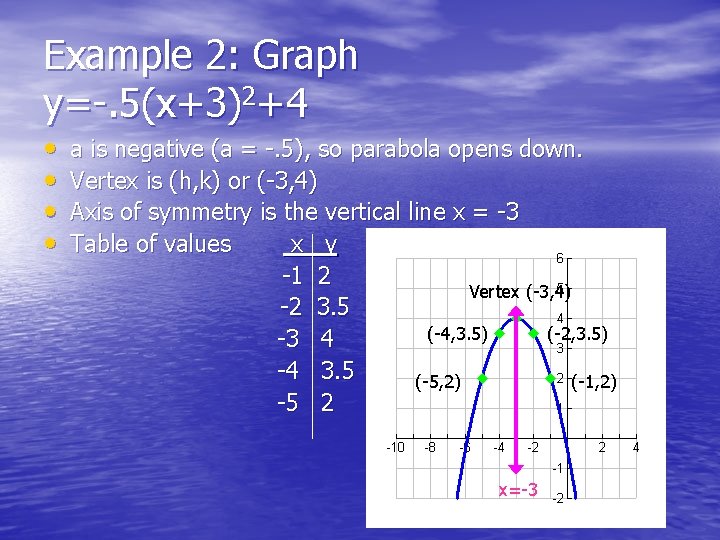
5 1 Graphing Quadratic Functions P 249 Definitions

Solution Write The Equation Y A X H 2 K With The Given With A Y Intercept 10 X Intercept 2 And Equation Of Axis X 3 0

Determine The Values Of H And K For Each Of The Following Transformations Write The Equation In The Form Y X H 2 K Sketch The Graph The Parabola Moves 3 Units Down And 2 Units

What Is The Vertex Of Y 3 X 6 2 4 Quora

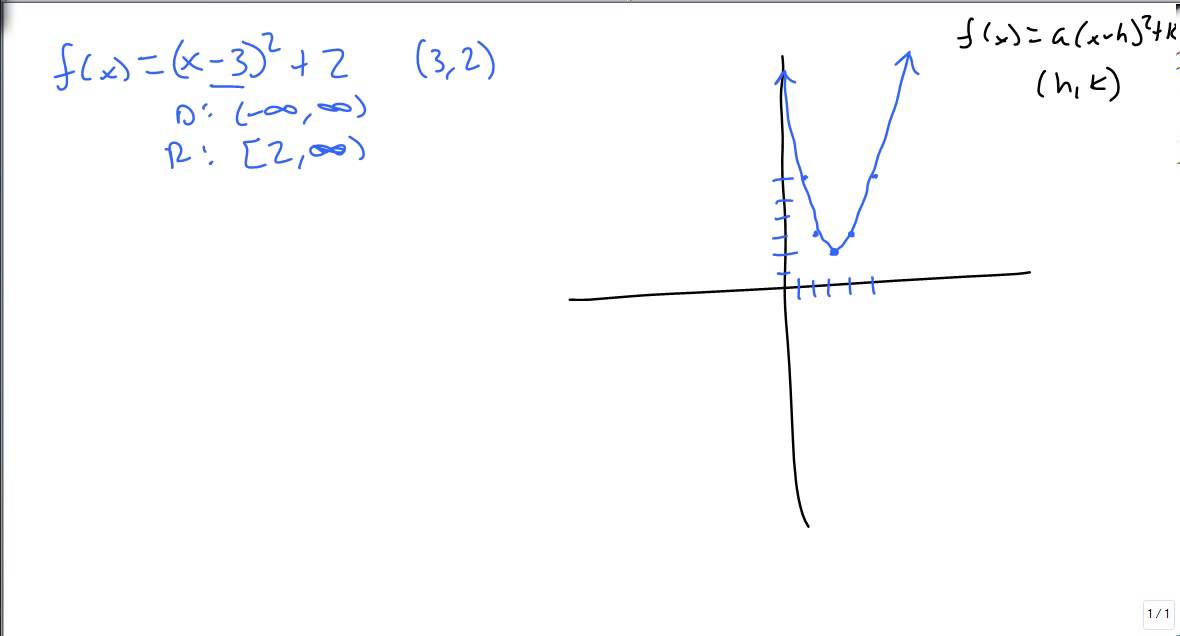
Graph By Transformations F X A X H 2 K Youtube

To Graph A Parabola We Need To Know The Coordinates Of Its Vertex Focus And The Equation Of Its Axis

Vertex Form How To Find The Equation Of A Parabola

Quadratic Functions

Solved Explain In Detail The Role Of A H And K In The Equation Y A X H 2 K You May Use Words Numerical Examples And Sketches To Suppo Course Hero

Solved The Parabola Y X 2 Is Transformed As Described Below Its Image Has The Form Y A X H 2 K Determine The Value Of A H And K For Each Transformation And Then Write The

Graphing Parabolas

Math Spoken Here About Quadratics 3

Graphing Parabolas