立体角は「$\theta=0$ の部分に対応する円」から「$\theta=\theta_0$ の部分に対応する円」までを集めたものの面積なので、 $\displaystyle\int_0^{\theta_0}2\pi\sin\theta d\theta\\ =2\pi(1\cos\theta_0)$ となります。 ちなみに、この公式は「光の単位」を変換するときにも現れます。立方体の表面積 計算式 立方体の表面積=一辺×一辺×6 円柱の表面積 計算式 円柱の表面積=底面積×2+底面の円周×高さ ※底面の円周=底面の円の直径×円周率(314) 球の表面積 計算式 球の表面積=半径×半径×円周率(314)×4 全国の中学校をお探しの方はこちらへ円すい(小)の母線=9cmが求められます。 24cm-9cm=15cmy 相似を利用した考え方 円すい(大)と取りさる円すい(小)の関係は相似 です。 ですから右の図のようになり、 ⑤=15cmと求められます。 円すい台の体積や表面積を求める方法には、

三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学
立体の表面積の求め方 公式
立体の表面積の求め方 公式-2/3時 ・ 相似な立体について、相似比と表面積の比、体積の比の関係を考察することができる。 本時の学習内容「立体の表面積や体積を、相似比と表面積の比、体積の比の関係を調べよう」を知る。 教科書133ページの「ひろげよう」を考える。 直方体 ・ 立体の表面積の考え方 ①展開図を考える ②底面積、側面積をそれぞれ求める ③底面積と側面積を足し合わせる ・ 角柱の表面積 表面積=底面積\(\times2\)側面積 ・ 円錐の表面積 表面積=底面積(円)側面積(おうぎ形) 今回はここまでです。




中1 数学 中1 立体の表面積 Youtube
数学16章空間図形「立体の表面積と体積」<準備問題①> 組 番 名前 面積や体積の表し方や求め方について,次の問いに答えなさい。 (1)次のア~ウの面積を求めなさい。 (1マス1㎝の方眼で,イの縦の長さは05㎝とする。) ア イ ウ 1㎝2し,その側面積を合計して全表面積とする長尾の方 法や されているが,この算出法は分子の立体構造が分配 係数に及ぼす影響を無視している.44) 舟崎らは cpk 分子モデルにより求めた分子表面積をA = 面積 P = 円周(近似式) 円錐 V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径
楕円体形状の腎臓動脈瘤の塞栓で、使用するコイルの適合サイズを表面積で推測するのに使用しました。 5 0913 60歳以上 / 会社員・公務員 / 非常に役に立った /漢字のとおり、立体の 「表面の面積」 のことだよ。 底面や側面など、 すべての面の面積 を求めて、たし合わせよう。 立体の表面積を求めるときのポイントは、これだよ。表面積の基本 表面積とは、立体の表面の面積を全て合わせた面積です。 基本的には、ひとつひとつの面の面積を地道に求めて足していきます。 はじめに、立体には面がいくつあって、どんな形になっているかを整理してから計算を始めると、間違いが少なくなりますよ! ひたすら面積を求めますので、面積の公式を頭に叩き込んでおいてください。 ( 面積の
動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru だから、円柱の表面積は、 (底面積)×2 側面積 で求められるってこと! さっそく、例題の表面積を求めてみよう。 底面が2つ、側面が1つだから、 9π×2 60π = 78π になるね! おめでとう!円柱の表面積の問題を瞬殺できるようになったね!!① 立体のすべての面の面積の和を表面積という。 また,側面全体の面積を側面積,1 つの底面の 面積を底面積という。 ②(柱体の体積)=(底面積)×(高さ),(柱体の表面積)=(側面積)+(底面




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者



1
中学数学球の体積の求め方の公式を1発で覚える方法 球の体積の求め方の公式が覚えられねえ!! こんにちは!この記事をかいているKenだよ。ビニール傘を買っちゃったね。 球の体積の求め方には公式があるんだ。 球の半径をrとすると、体積の求め方第6章空間図形立体の表面積の問題の解答。 1 右図の四角柱の表面積を求めなさい。 家庭教師のガンバは、勉強が嫌いな子、勉強が苦手な子、勉強のやり方がわからない子を中心に年以上運営されている家庭教師センターです。立方体の辺の長さから体積と表面積を計算します。 立方体の辺の長さ 立方体の辺の長さ 立方体の体積から辺の長さと表面積を計算します。 直方体の体積 直方体の体積 直方体の三辺の長さから体積と表面積を計算します。 四面体の体積 四面体の体積
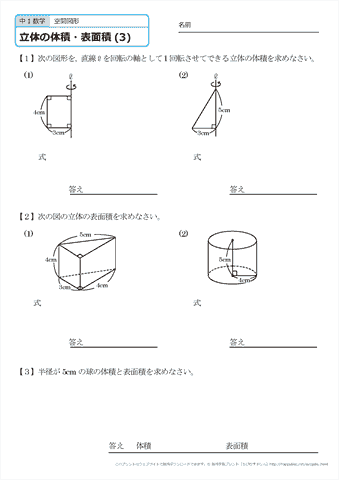



中学1年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




角錐 円錐の体積と表面積の公式 数学fun
立方体の公式と計算(求め方) 立方体の公式を下記に示します。 立方体の体積=a 3 aは1辺の長さです。その他の立体図形の体積の算定は下記が参考になります。 体積の公式は?1分でわかる求め方と覚え方、一覧、三角柱、円柱、三角錐の体積表面積の意味、求め方は下記も参考になります。 表面積とは?近日公開予定 立方体の公式は?1分でわかる意味、体積の公式と例題の求め方、表面積の公式 100円から読める!ネット不要!印刷しても読みやすいpdf記事はこちら⇒ いつでもどこでも円柱の表面積を求める公式は、次の通りです。 S = 2πr2 2πrh = 2πr(r h) S = 2 π r 2 2 π r h = 2 π r (r h) ここで、S は円柱の表面積、π は円周率、r は底面の円の半径、h は高さを表します。




円錐の表面積の求め方 公式と計算例




三角柱の体積の求め方 小学生向けに問題使って解説するぞ 中学数学 理科の学習まとめサイト
0•r•acosµg r 1 r2 a2 ¡r2 rdrdµ となる。これを計算して、S = 2a2 ¡2 が得られる。 練習131 球面x 2 y 2 z2 = a の表面積を求めよ。( z = p a ¡x2 ¡y2 の fx2 y2 • a2g 上の曲面積の2倍)典型的な図形であり、十分論証的に求められている。 これらの基本的な部分形は少数の これらを西洋流の定理のように用い て、複雑な立体の体積・表面積に適用し、幾何学的な解釈によって求積しよう立体と空間図形 1次の(1)~(4)の立体について下の表を完成させなさい。 3面積(表面積)の求め方について、下の( )に当てはまる言葉を入れなさい。 (1) 面積(表面積)の単位はcm2 (2) 正方形の面積 = 一辺の長さ×一辺の長さ




表面積の求め方 計算公式一覧




表面積の求め方 計算公式一覧
1/3時 ・角柱や円柱の表面積を求めることができる。 ・角柱や円柱の表面積の求め方を理解する。 本時の学習内容「角柱や円柱の表面積の求め方を考えよう」を知る。 教科書143ページの「考えてみよう」に取り組む。 立体の「表面積」、「底面積¡x2 ¡y2 であることから求める曲面積は、上下の対称性から S = 4 Z Z f0•µ• 2;立体・表面積・基礎★★★ 表面積の計算面倒ですね~。 計算が合わないときも多いですし。 それでもどうすれば楽にきれいに解けるかを常に考えましょう! 表面積の求め方 問題 下の(1)~(3)の立体図形の表面積を求めなさい。




空間図形14 円すい台の体積 Youtube



斜めに切った円柱や角柱の体積を求める方法 中学受験ー算数解き方ポータル
中1 数学 表面積の求め方 表面積の求め方と!円錐の側面積と中心角の簡単な裏ワザをごしょーかい!ページ数少ないです笑 塾で教えてもらいました(((( 学年 中学1年生, 教科書 新編 新しい数学1 東京書籍, 単元 立体の体積と表面積, キーワード 中1,数学,表面積,求め方,まとめ,裏ワザ,簡(15年秋田県立高校入試問題) π(cm2) 立体は円柱になり,表面積は底面積×2=16π×2(cm2)と側面積8π×7(cm2)の合計になります 底面積2つで32π(cm2),側面積56π(cm2)の合計はπ(cm2)(答)立体の体積 角柱、円柱の体積 柱の体積 = 底面積 × 高さ (例) 三角柱 高さ8cm 底面積 5cm 2 体積=5×8=40 四角柱(直方体) 4cm 3cm 8cm 底面積=4×3=12 体積=12×8=96 半径5cm 高さ 8cm 円柱 底面積=5×5×π=25π 体積=25π×8=0π 例題次の立体の体積を求めよ。 底面積15cm 2, 高さ6cmの五角柱 底面の半径2cm, 高さ10cm




中学数学 円錐の高さの求め方 頻出パターン なぜか分かる はかせちゃんの怪しい研究室




3分でなるほど 三角錐の体積 表面積の求め方をマスターしよう 数スタ
次に、円柱の表面積の求め方は「底面積 × 2 側面積」なので、式は「4π × 2 側面積」。 また、円柱の側面積の求め方は「高さ × 円周」、円周の求め方は「直径 × π」なので、式にすると 4π × 2 8 × 4π = 40π なので、表面積は 40π($cm^2$)となります。立体の表面積 → 携帯版は別頁 == 立体の表面積展開図(入試問題) == 要点11 ≪円柱の側面積≫ 円柱の表面積は,2つの底面積と側面積の和になります. 右図のように底面の半径が r ,高さが h である円柱の側面は長方形で,側面積は 2πr×h になります. ※以下に引用している入試問題で,元の問題は記述式ですが,この教材ではWeb上での操作性をよくする 今回は立体図形の1つ、円柱の表面積の求め方について書きたいと思います。 円柱の表面積の求め方公式 円柱の表面積を求めるときには展開図をイメージ 円柱の表面積を求める問題 問題① 《円柱の表面積の求め方》 問題② 《円柱の表面積の求め方》 問題③ まとめ スポンサードリンク




計算公式 立方体の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




中1数学 立体の表面積 について 空間図形 ひっそりと物理や数学を解説する
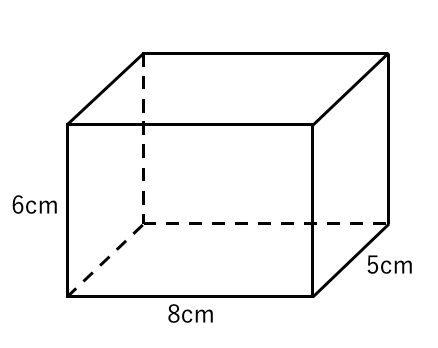
立方体の12の辺の長さは等しく、これを $a$ とします。立方体の表面積 $S$ は、次の式で求められます。 立方体の表面積 \begin{align*} V = 6a^2 \end{align*} 表面積 = 一辺 × 一辺 × 6




簡単 三角錐の体積 表面積の求め方と展開図が誰でもすぐわかる記事 高校生向け受験応援メディア 受験のミカタ




中1数学 三角柱 四角柱の体積の求め方がサクッとわかる 映像授業のtry It トライイット




体積 複雑な形の立体 算数 教科質問ひろば 進研ゼミ小学講座



円錐 体積 求め 方 公式を図解 すい体の体積 円すいの表面積の求め方 Amp Petmd Com




円柱 の 求め 方 円柱の体積の求め方 公式 Amp Petmd Com




三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学




公式を図解 すい体の体積 円すいの表面積の求め方




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
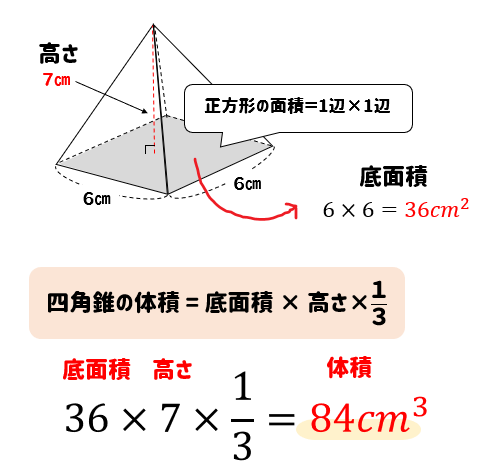



3分でなるほど 四角錐の体積 表面積の求め方をマスターしよう 数スタ




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




中1数学 立体の表面積と体積の求め方と練習問題 Pikuu




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン




3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ




中3 三角形の相似 円錐の体積比 日本語版 Youtube




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強




円柱の表面積と体積を求める公式 具体例で学ぶ数学



1




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




円錐の表面積 Youtube



1




円錐の体積ってなんであの公式なの Webty Staff Blog




中1 数学 6 5 球の体積 表面積 Youtube




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




球の表面積と体積の公式 数学fun




表面積の求め方 計算公式一覧




角柱 円柱の表面積と体積の公式 数学fun



立体の体積と表面積 1 柱体の表面積




円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題




中1 数学中2 立体の体積と表面積 公式 中学生 数学のノート Clear
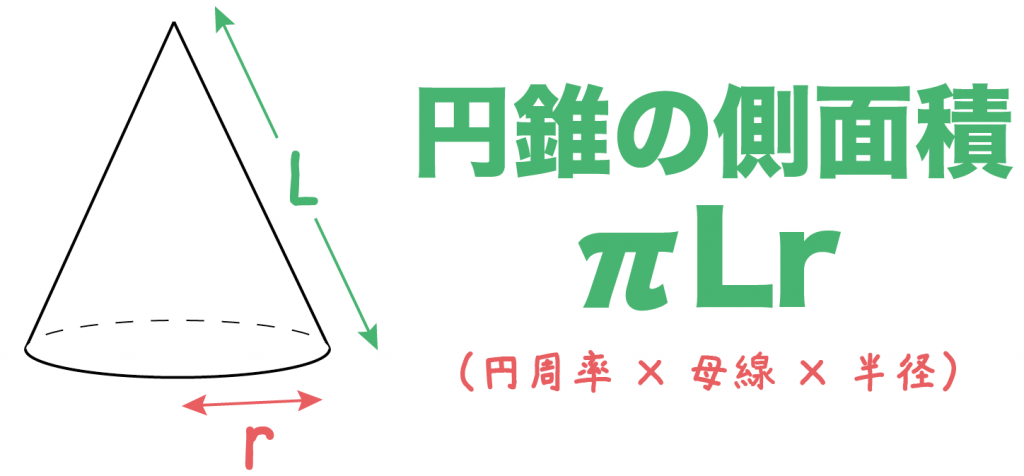



簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
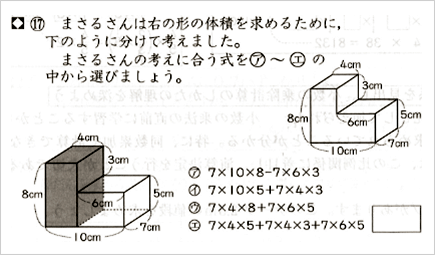



直方体や立方体の体積 児童が既習の知識と結び付けて考察できる授業を目指して 私の実践 私の工夫アーカイブ一覧 授業支援 サポート資料 算数 小学校 知が啓く 教科書の啓林館




公式を図解 すい体の体積 円すいの表面積の求め方




小6 算数 小6 26 角柱と円柱の体積 基本編 Youtube




中1数学 立体の体積 練習編 映像授業のtry It トライイット



数学の問題教えてください 立方体から切り取った三角錐の体積はどうやって Yahoo 知恵袋
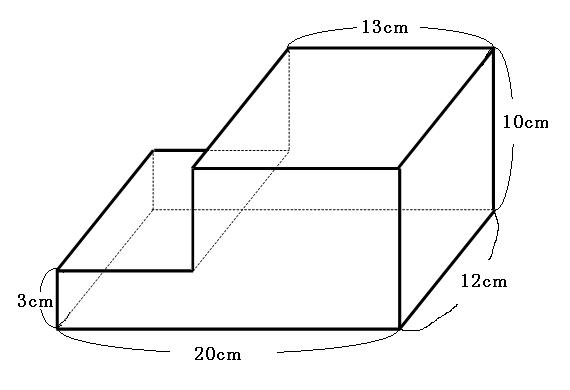



立体の表面積の求め方を解説 面倒な角柱や円柱の表面積をいかにサボって求めるか




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強




中1 数学 中1 立体の体積 Youtube




中1 数学 中1 立体の表面積 Youtube




公式を図解 すい体の体積 円すいの表面積の求め方



Studydoctor円錐の表面積の求め方 中学1年数学 Studydoctor




角錐 円錐の体積と表面積 計算ドリル 問題集 数学fun



5 5 複雑な立体の表面積と面積を求めるには さんすうがく




立方体 直方体の体積の求め方 小学生に教えるための分かりやすい解説 数学fun
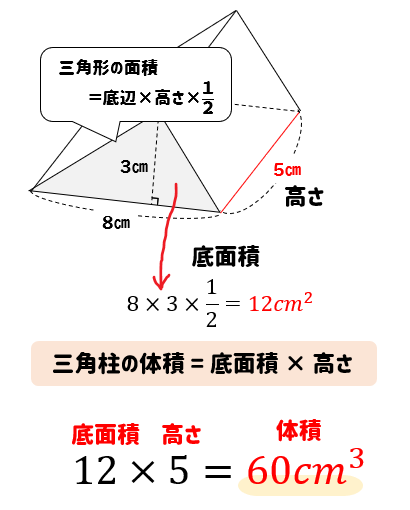



3分でなるほど 三角柱の体積 表面積の求め方をマスターしよう 数スタ




スタディピア 立体の表面積




空間図形 円柱の側面積の求め方がわかりません 中学数学 定期テスト対策サイト




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学



下の図の円すいと円柱を合わせた立体の体積を求めなさい なお 円周率はpを用いる Yahoo 知恵袋




三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学




中学1年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




円錐 体積 求め 方 公式を図解 すい体の体積 円すいの表面積の求め方 Amp Petmd Com




角錐 円錐の体積 Youtube




円柱の計算 体積 表面積の求め方はこれでバッチリ 数スタ
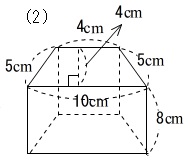



表面積や体積の求め方 三角柱 四角柱 円柱 球や半球
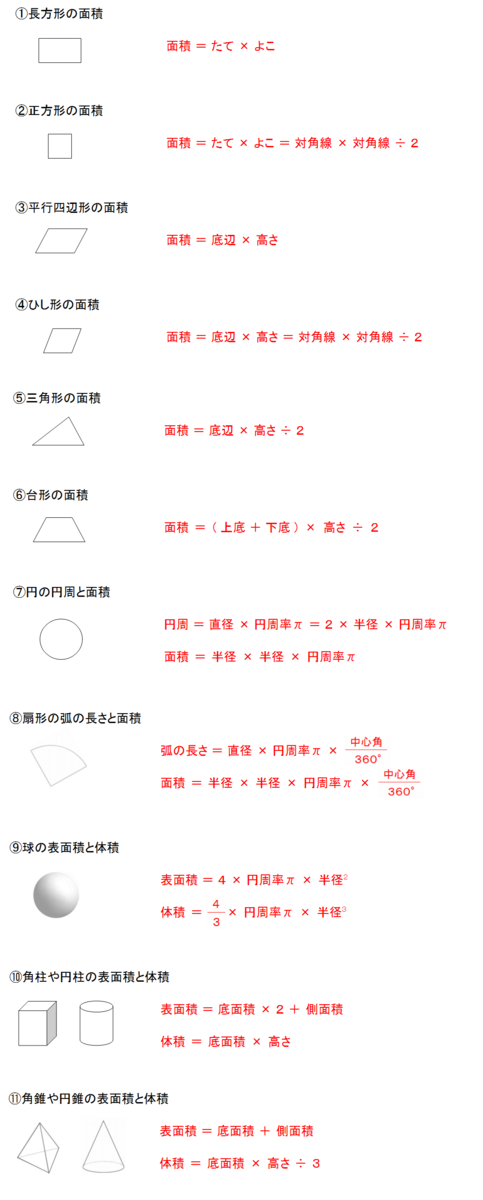



図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師




中1 中1 数学まとめ 立体の体積や表面積など 中学生 数学のノート Clear




三角柱の体積 表面積の求め方が図で誰でも即わかる 展開図も紹介 高校生向け受験応援メディア 受験のミカタ



立体の表面積




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



Studydoctor柱体や角錐の表面積の求め方 中学1年数学 Studydoctor



1




計算公式 三角柱の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン




中学1年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



立体の体積を求める 苦手な数学を簡単に



立方体の表面積の求め方は 1分でわかる計算 公式 直方体の表面積の求め方




3分でなるほど 四角柱の体積 表面積の求め方をマスターしよう 数スタ




立方体の表面積と体積を求める公式と計算問題 単位との関係も ウルトラフリーダム




球の表面積と体積の公式 数学fun



立体 の 表面積 求め 方




表面積の求め方 計算公式一覧



写真の底面が扇形の立体の表面積の求め方を教えてください 特に側面積が Yahoo 知恵袋




円錐の体積を求める Youtube




小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生




角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強




円柱を2つ重ねた立体の表面積の求め方 Qikeru 学びを楽しくわかりやすく



球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典




計算公式 円柱の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



6年算数立体の体積その2 教え方




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




中1 中1数学 球の体積と表面積 中学生 数学のノート Clear




2 を途中式を含めて教えてください Clear
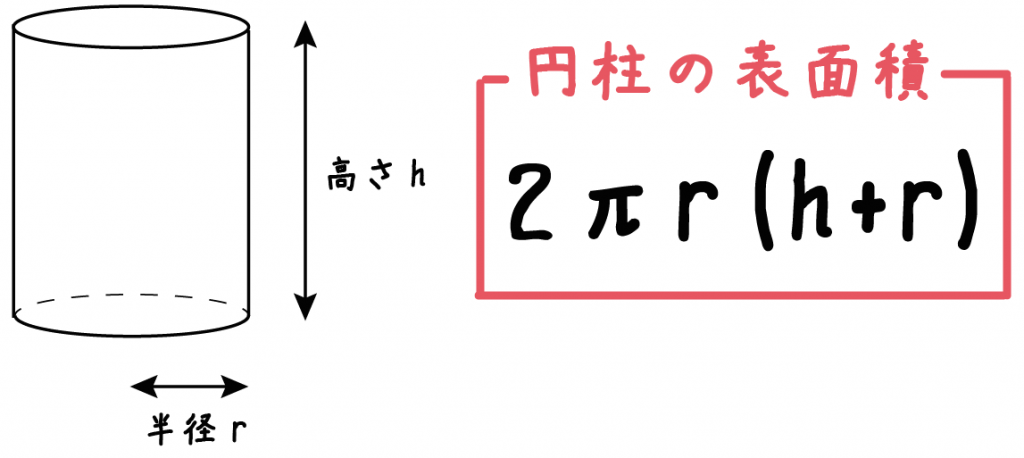



簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




三角柱の底面積 側面積 表面積の求め方 具体例で学ぶ数学




小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生



0 件のコメント:
コメントを投稿