The fact tells us that this line integral should be the same as the second part ( ie zero) However, let's verify that, plus there is a point we need to make here about the parameterization Here is the parameterization for this curve C 3 → r ( t) = ( 1 − t) 1, 1 t − 1, 1 = 1 − 2 t, 1 for 0 ≤ t ≤ 1 Now, using Green's theorem on the line integral gives, ∮ C y 3 d x − x 3 d y = ∬ D − 3 x 2 − 3 y 2 d A ∮ C y 3 d x − x 3 d y = ∬ D − 3 x 2 − 3 y 2 d A where D D is a disk of radius 2 centered at the origin Since D D is a disk it seems like the best way toThe base is the region enclosed by y = x 2 y = x 2 and y = 9 y = 9 Slices perpendicular to the xaxis are right isosceles triangles The intersection of one of these slices and the base is the leg of the triangle 73 The base is the area between y = x y = x and y = x 2 y = x 2
Find The Area Of The Segment Cut Off From The Parabola Y 2 2x By The Line Y 4x 1 Sarthaks Econnect Largest Online Education Community
The line x+y=2 cuts the parabola
The line x+y=2 cuts the parabola- Prove that the curves x = y 2 and xy = k cut at right angles if 8k 2 = 1 Hint Two curves intersect at right angle if the tangents to the curves at the point of intersection are perpendicular to each other Example 2 y = x 2 − 2 The only difference with the first graph that I drew (y = x 2) and this one (y = x 2 − 2) is the "minus 2" The "minus 2" means that all the yvalues for the graph need to be moved down by 2 units So we just take our first curve and move it down 2 units Our new curve's vertex is at −2 on the yaxis



What Is The Distance Between Two Points If X Y 1 Cuts Circle X 2 Y 2 1 At Two Points Quora
Find the volume and surface area of a solid of revolution that is generated by rotating the area between the yaxis, y = 0, the line y = 1 and the parabola y = x 2 about the yaxis Plot the Area Clearly, the area is the parabola y = x 2 cut in half and topped by the line y = 1M = 68 m = 78 m = 102 m = 112 c What is the equation, in pointslope form, of the line that is perpendicular to the given line and passes through the point (2, 5)?Surface area and surface integrals (Sect 165) I Review Arc length and line integrals I Review Double integral of a scalar function I The area of a surface in space Review Double integral of a scalar function I The double integral of a function f R ⊂ R2 → R on a region R ⊂ R2, which is the volume under the graph of f and above the z = 0 plane, and is given by
Let f (x,y)=1/ (x^2y^2) for (x,y)\neq 0 Determine whether f is integrable over U0 and over \mathbb {R}^2\bar {U};Answer to Evaluate \iint_S \sqrt {4y 1} ds where S is the first octant part of y = x^2 cut out by 2x y z = 1 By signing up, you'll getAssignment 7 (MATH 215, Q1) 1 Find the area of the given surface (a) The part of the cone z = p x2 y2 below the plane z = 3 Solution The surface can be represented by the vector equation
If so, evaluate Let f (x,y) = 1/(x2 y2) for (x,y) = 0 Determine whether f is integrable over U −0 and over R2 −U ˉ;To y= x2 4, whereas for washers the inner and outer sides would both be determined by y= 4 x2 on the top half of the solid and by y= x 2 4 on the bottom half of the solid Since we're using cylindrical shells and the region runs from x= 2 to x= 2, the volume of the solidY= x 2 z cut o by the plane y= 25 Solution Surface lies above the disk x 2 z in the xzplane A(S) = Z Z D p f2 x f z 2dA= Z Z p 4x2 4y2 1da Converting to polar coords get Z 2ˇ 0 Z 5 0 p 4r2 1rdrd = ˇ=8(101 p 101 1) Section 167 2




3 The Equation Of Straight Line Cutting Off An Intercept 2 From Y Axis And Being




Find The Find The Oour On Oth 0 E A B N V 2 10 0 At The Points N B Nthe Line 2 X 5 Y 1 Meets The Curve X 2 5 X
Find the slope of the tangent to a parabola y = x 2 at a point on the curve where x = ½ A 0 93 Find the acute angle that the curve y = 1 – 3x 2 cut the xaxisY= x2 left of x= 1 We reverse the order of integration, so that Z 1 0 Z 1 p y p x3 1 dxdy= Z 1 0 Z x2 0 p x3 1 dydx = Z 1 0 x2 p x3 1 dx = 2 9 (x3 1)3=2j1 0 = 2 9 (23=2 1) c) The integral representing the volume bounded by ˆ= 1 cos˚(in spherical coordinates)X162 Line Integrals 1 Line Integral with respect to the arc length Consider a planar curve C given by r(t) = hx(t), y(t)i, a t b Divide the parameter interval a,b into n subintervals t i 1,t i, i = 0, ,n, and thus divide the curve C correspondingly n subcurves of length Ds




If The Line Y Mx M 1 Cuts The Circle X 2 Y 2 4 At Two R




The Slope Of The Tangent To The Curve Y X 2 X At The Point Where The Line Y 2 Cuts The Curve In The Brainly In
If the Curve Ay X2 = 7 and X3 = Y Cut Orthogonally at (1, 1), Then a is Equal to (A) 1 (B) −6 6 (D) 0 Mathematics Advertisement Remove all ads Advertisement Remove all adsClick here👆to get an answer to your question ️ If the line y √(3)x 3 = 0 cuts the parabola y^2 = x 2 at A and B , the PA PB is equal to If P = √(3), 0) Ex 63, 23 Prove that the curves 𝑥=𝑦2 & 𝑥𝑦=𝑘 cut at right angles if 8𝑘2 = 1We need to show that the curves cut at right angles Two Curve intersect at right angle if the tangents to the curves at the point of intersection are perpendicular to each other First we Calculate the point of inters



Solved The Straight Line Y X 4 Cuts The Circle X 2 Y 2 26 At P And Q A Calculate The Coordinates Of P And Q B Sketch The Circle And T Course Hero



Search Q The Equation Y 3d5 In Two Variables Can Be Written As Tbm Isch
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historySolution Steps y = x2 y = x − 2 Swap sides so that all variable terms are on the left hand side Swap sides so that all variable terms are on the left hand side x2=y x − 2 = y Add 2 to both sides Add 2 to both sides If the curves ay x^2 = 7 and y = x^3 cut each other orthogonally at a point, find a asked in Limit, continuity and differentiability by SumanMandal ( 546k points) the tangent and normal




Ex 8 1 7 Find Area Of Smaller Part Of Circle X2 Y2 Cutoff




Solved Parametrize The Surface S S Is The Cap Cut From T Chegg Com
Rewrite as x^22xy=0 This is a quadratic equation in variable x Don't be confused, I'm just pointing out that we will temporarily be thinking of y as a constant (a number) We would solve by factoring if we could, but we can't so we'll use the quadratic formula, which says that the solutions to 2x^2 bx c = 0 are x=(bsqrt(b^24ac))/(2a)This is the 3rd video I sent to a graduating Grade 12 when her graduation in was cancelled because of COVID19 Her Mom asked those who knew her or taugCalculus Multivariable Calculus Find the area of the finite part of the paraboloid y = x 2 z 2 cut off by the plane y = 25 Hint Project the surface onto the xzplane more_vert Find the area of the finite part of the paraboloid y = x 2 z 2 cut off by the plane y
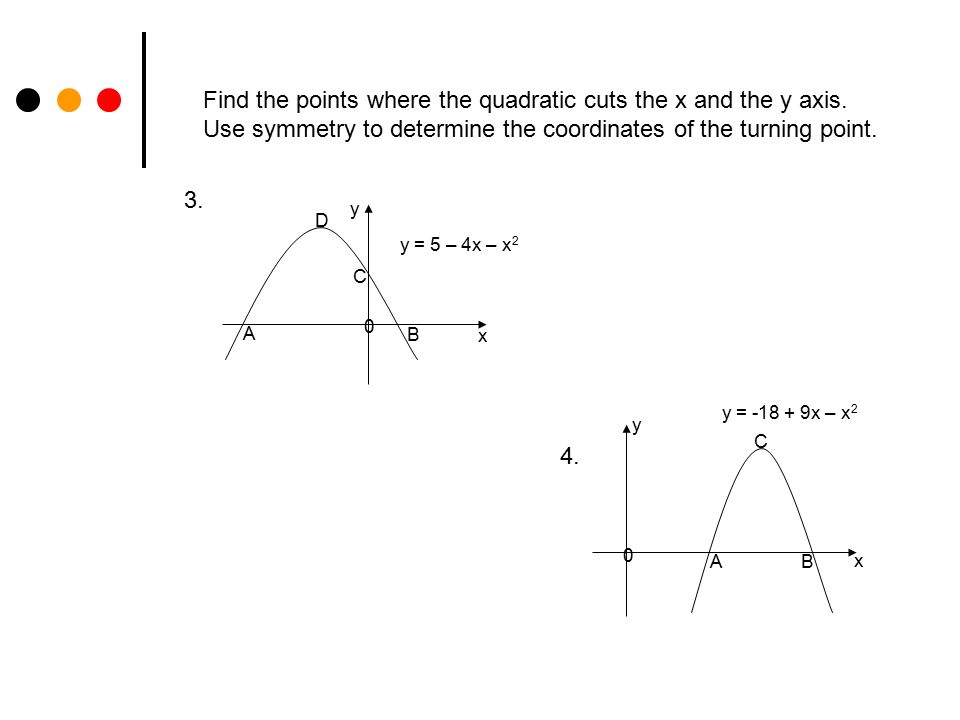



Quadratics Cutting Axis 2 Algebra Quadratics Cutting The X And Y Axis In Each Of The Examples Which Follow You Are Asked To A Find The Points Where Ppt Download




If A Circle Passes Through A Point 1 2 And Cut The Circle X 2 Y
Divide 0 0 by 4 4 Multiply − 1 1 by 0 0 Add − 2 2 and 0 0 Substitute the values of a a, d d, and e e into the vertex form a ( x d) 2 e a ( x d) 2 e Set y y equal to the new right side Use the vertex form, y = a ( x − h) 2 k y = a ( x h) 2 k, to determine the values of a a, h h, and k kHi Mike, y = x 2 2 is a quadratic equation of the form y = ax 2 bx c, let a = 1, b = 0 and c = 2 You can certainly plot the graph by using values of x from 2 to 2 but I want to show you another way I expect that you know the graph of y = x 2 If you compare the functions y = x 2 and y = x 2 2, call them (1) and (2), the difference is that in (2) for each value of x the You have x2 −y2 = (x y)(x −y) So in your case x2 − y2 x −y = (x y)(x − y) x − y = x y Answer link



14 3 Partial Differentiation



How Do You Write The Definite Integral To Find The Class 12 Maths Cbse
If so, evaluate https//mathstackexchangecom/q/For positive values of a and b, the binomial theorem with n = 2 is the geometrically evident fact that a square of side a b can be cut into a square of side a, a square of side b, and two rectangles with sides a and bWith n = 3, the theorem states that a cube of side a b can be cut into a cube of side a, a cube of side b, three a × a × b rectangular boxes, and three a × b × bSo, other point where parabola will cut the straight line is when x is 2, in which case y = x^2 = (2)^2 = 4 So, second point is (2, 4)



Solved The Length Of The Chord Cut Off By Y 2x 1 From The Circle X 2 Self Study 365




Draw The Graph Of The Equation 2x Y 6 Find The Coordinates Of The Graph Cut The X Axis
3,304 2 i think you dropped a sign somewhere, but i would go as follows x 2 y 2 = x 2 y 2 0 = x 2 y 2 ( (xy) (xy)) = x 2 xy xy y 2 but as I think Mark was pointing out, all the steps you took working from RHS to LHS are perfectly valid in Here we can clearly see that the quadratic function y = x^{2} does not cut the xaxis But the graph of the quadratic function y = x^{2} touches the xaxis at point C (0,0) Therefore the zero of the quadratic function y = x^{2} is x = 0 Now you may think that y = x^{2} has one zero which is x = 0 and we know that a quadratic function has 2 zerosOver the region D = {(x,y) x2 y2 8} As before, we will find the critical points of f over DThen,we'llrestrictf to the boundary of D and find all extreme values It is in this second step that we will use Lagrange multipliers The region D is a circle of radius 2 p 2
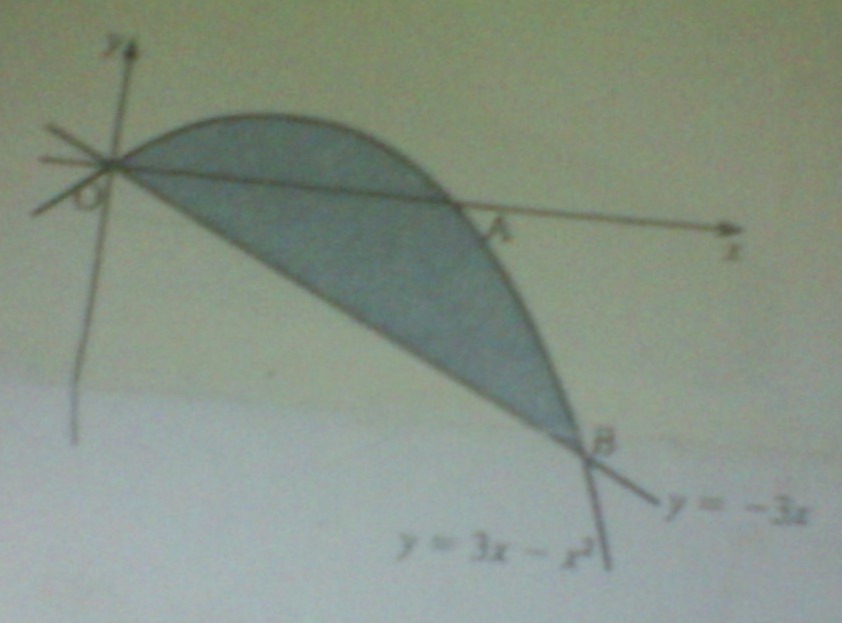



The Curve Y 3x X 2 Cuts The X Axis At The Points O And A And Meets The Line Y 3x At The Point B As In The Diagram A Calculate The Coordinate Of A




At Which Point The Graph Of The Linear Equation 2x Y 7 Cuts On Y Axis Brainly In
X 2 ( 1 2 y) x y 2 y − 2 Find one factor of the form x^ {k}m, where x^ {k} divides the monomial with the highest power x^ {2} and m divides the constant factor y^ {2}y2 One such factor is xy1 Factor the polynomial by dividing it by this factorStart your free trial In partnership withGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!




Volume The Plane X A Y B Z C 1 A 0 B 0 Chegg Com




If The Line Y Sqrt3 X 3 0 Cuts The Parabola Y 2 X 2 At A And B Then Find The Value Of Youtube
This is always true with real numbers, but not always for imaginary numbers We have ( x y) 2 = ( x y) ( x y) = x y x y = x x y y = x 2 × y 2 (xy)^2= (xy) (xy)=x {\color {#D61F06} {yx}} y=x {\color {#D61F06} {xy}}y=x^2 \times y^2\ _\square (xy)2 = (xy)(xy) = xyxy = xxyy = x2 ×y2 For noncommutative operators under some algebraicAnswer to Find the area of the finite part of the paraboloid y = x^2 z^2 cut off by the plane y = 81 (Hint Project the surface onto theCalculus Calculus Early Transcendentals Find the area of the finite part of the paraboloid y = x 2 z 2 cut off by the plane y = 25 Hint Project the surface onto the xzplane more_vert Find the area of the finite part of the paraboloid y = x 2 z 2 cut off by the plane y = 25 Hint Project the surface onto the xzplane



Count Number Of Triangles Cut By The Given Horizontal And Vertical Line Segments Geeksforgeeks




The Graph Of Linear Equation X 2y 2 Cuts The Y Axis At O 2 0 O 0 2 O 1 1 0 1 Brainly In
Equation of a Straight Line 11 Solve y3x2 = 0 Tiger recognizes that we have here an equation of a straight line Such an equation is usually written y=mxb ("y=mxc" in the UK) "y=mxb" is the formula of a straight line drawn on Cartesian coordinate system in which "y" is the vertical axis and "x" the horizontal axis In this formulaFind the area of the finite part of the paraboloid y = x2 z2 cut off by the plane y = 16 Hint Project the surface onto the xzplane Expert Answer % (16 ratings) Previous question Next question Get more help from Chegg Solve it with our calculus problem solver and calculatorCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history



What Is The Distance Between Two Points If X Y 1 Cuts Circle X 2 Y 2 1 At Two Points Quora




Find The Surface Area Of The Surface Cut From The Paraboloid X 2 Y 2 Z 0 By The Plane Z Study Com
Y = x 2 2 First, we find the critical points on D We begin by finding the partials and setting them equal to zero • fx(x,y)=1y =0 • fy(x,y)=1x =0 The only critical point on D is (1,1) Notice that f(1,1) = 1 Now, we find the extreme points on the boundary We will use the information in our picture to help us From (0 ,0) to (0,2), theRelated » Graph » Number Line » Examples » Our online expert tutors can answer this problem Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!What must be the value of x so that lines c and d are parallel lines cut by transversal p?



Solved The Straight Line Y X 4 Cuts The Circle X 2 Y 2 26 At P And Q A Calculate The Coordinates Of P And Q B Sketch The Circle And T Course Hero
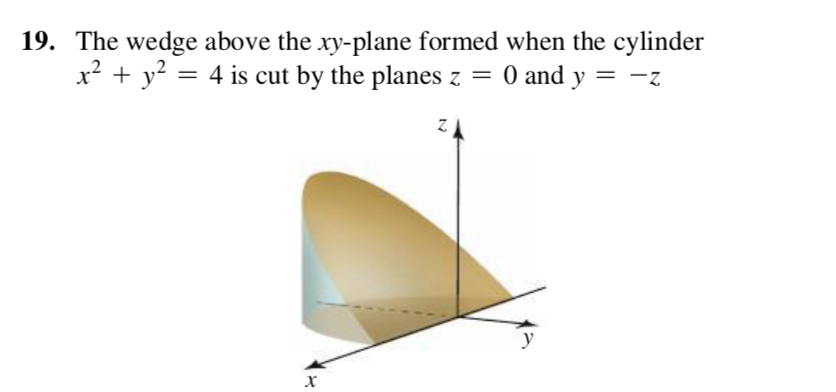



19 The Wedge Above The Xy Plane Formed When The Chegg Com
Factor x^2y^2 x2 − y2 x 2 y 2 Since both terms are perfect squares, factor using the difference of squares formula, a2 −b2 = (ab)(a−b) a 2 b 2 = ( a b) ( aFor graph Y = x^2 Kx 2 to cut x axis y coordinate must be zero thus, x^2 Kx 2 = 0 Now for this equation for solution to be finitly 2 , b^2 4ac > 0 here b = K , a = 1 and c = 2 for every value of K , b^2 4ac will be greater than zero for example k = 0 => (0)^2 4(1)(2) = 8 for k = 1 => (1)^2 4(1)(2) = 912 18 81 99 b Two parallel lines are crossed by a transversal What is the value of m?




If The Plane X 2 Y 3 Z 4 1 Cuts The Coordinate Axes In A B C Then The Area Of Triangle Youtube



Draw The Graph Of The Linear Equation 3x 4y 6 At What Points Does The Graph Cut The X Axis And The Y Axis Studyrankersonline
Y = 12 x^2, y = x^2 6Sketch the region enclosed by the given curves Decidewhether to integrate with respect to x or y Draw a typical approximatingrectaExample 57 Find the area of the ellipse cut on the plane 2x 3y 6z = 60 by the circular cylinder x 2 = y 2 = 2x Solution ThesurfaceS liesin theplane 2x3y6z = 60soweusethisto calculatedS =Solve Quadratic Equation by Completing The Square 22 Solving x26x10 = 0 by Completing The Square Subtract 10 from both side of the equation x26x = 10 Now the clever bit Take the coefficient of x , which is 6 , divide by two, giving 3 , and finally square it giving 9 Add 9 to both sides of the equation On the right hand side we have




Left Ion Dipole Electrostatic Energy V R R 3 R X 2 Y 2 Download Scientific Diagram




If The Circle X 2 Y 2 2x 3y 1 0 Cuts X 2 Y 2 4x 3y 2 0 At




Equation Wikiwand




The Graph Of Linear Equationx 2y 2 Cuts The Y Aris At Brainly In




The Graph Of The Linear Equation 2x Y 4 Cuts X Axix At A 2 0




Draw The Graph Of The Equation 3x 2y 6 Find The Coordinates Of The Point Where The Graph Cuts The Y Axis




Find The Equation Of The Tangent To The Curve Y X 7 X 2 X 3




Graph Of Z 1 X 2 Y 2 Novocom Top




The Wedge Cut From A Cylinder X 2 Y 2 1 By The Planes Z Y And Z 0 1 Sketch The Region Of Integration And Find The Bounds 2




Find The Volumes Of The Regions The Region Cut From The Cylinder X 2 Y 2 4 Youtube



Find The Equation Of Tangent To The Curve Y X 7 X 2 X 3 At The Point Where It Cuts The X Axis Sarthaks Econnect Largest Online Education Community




11 A Digraph With 2 Cut X Y Neither Of The Bridges Of This 2 Cut Download Scientific Diagram
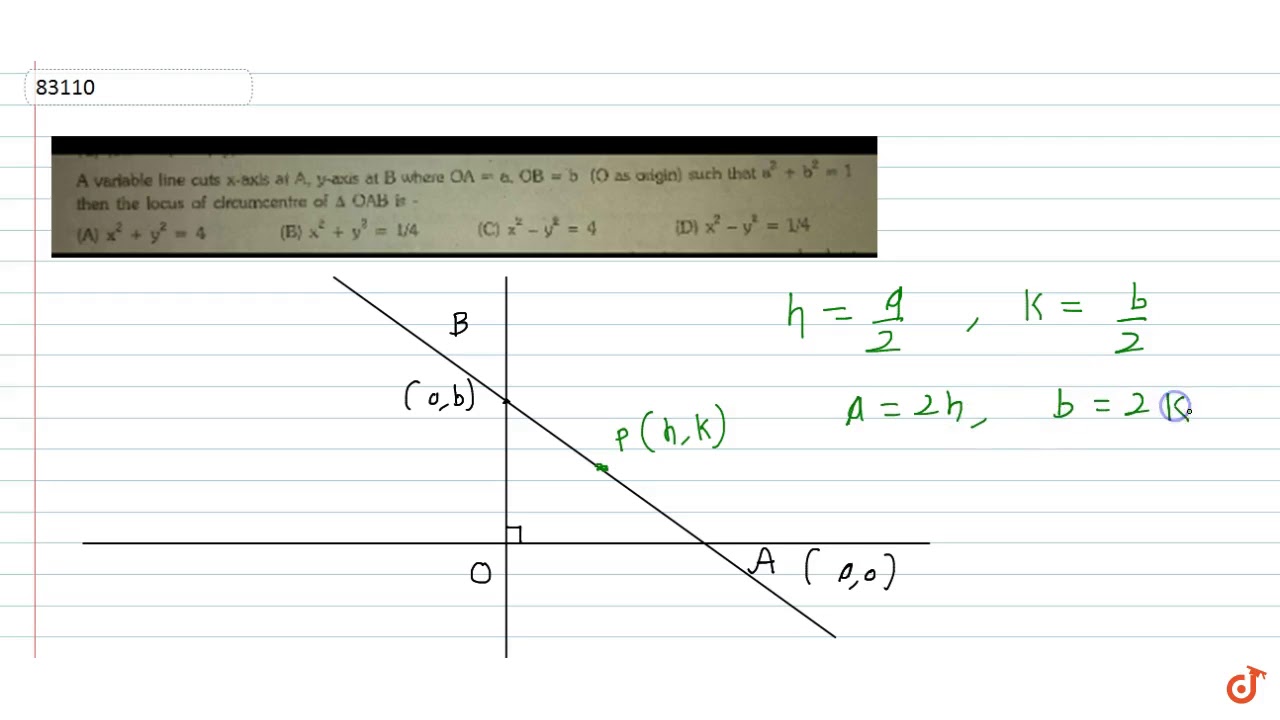



A Variable Line Cuts X Axis At A Y Axis At B Where Oa A Ob B O As Origin Such That Then Youtube




3 The Figure Shows The Curve See How To Solve It At Qanda




Which One Of The Following Curves Cut The Parabola



Q Tbn And9gcrbi9blo Wofvbzwqyztuiacedgeo1l24bjehodcy52fa23rbjt Usqp Cau




Find The Area Of The Smaller Part Of The Circle X 2 Y 2 A 2 Cut Off By The Line X A Sqrt 2 Youtube



Find The Area Of The Segment Cut Off From The Parabola Y 2 2x By The Line Y 4x 1 Sarthaks Econnect Largest Online Education Community



The Line Y X 2 Cuts The Curve 2x 2 Y 2 5xy 8 At A And B What Are The Coordinates Of The Midpoint Of Ab Quora




Graphs Of Surfaces Z F X Y Contour Curves Continuity And Limits
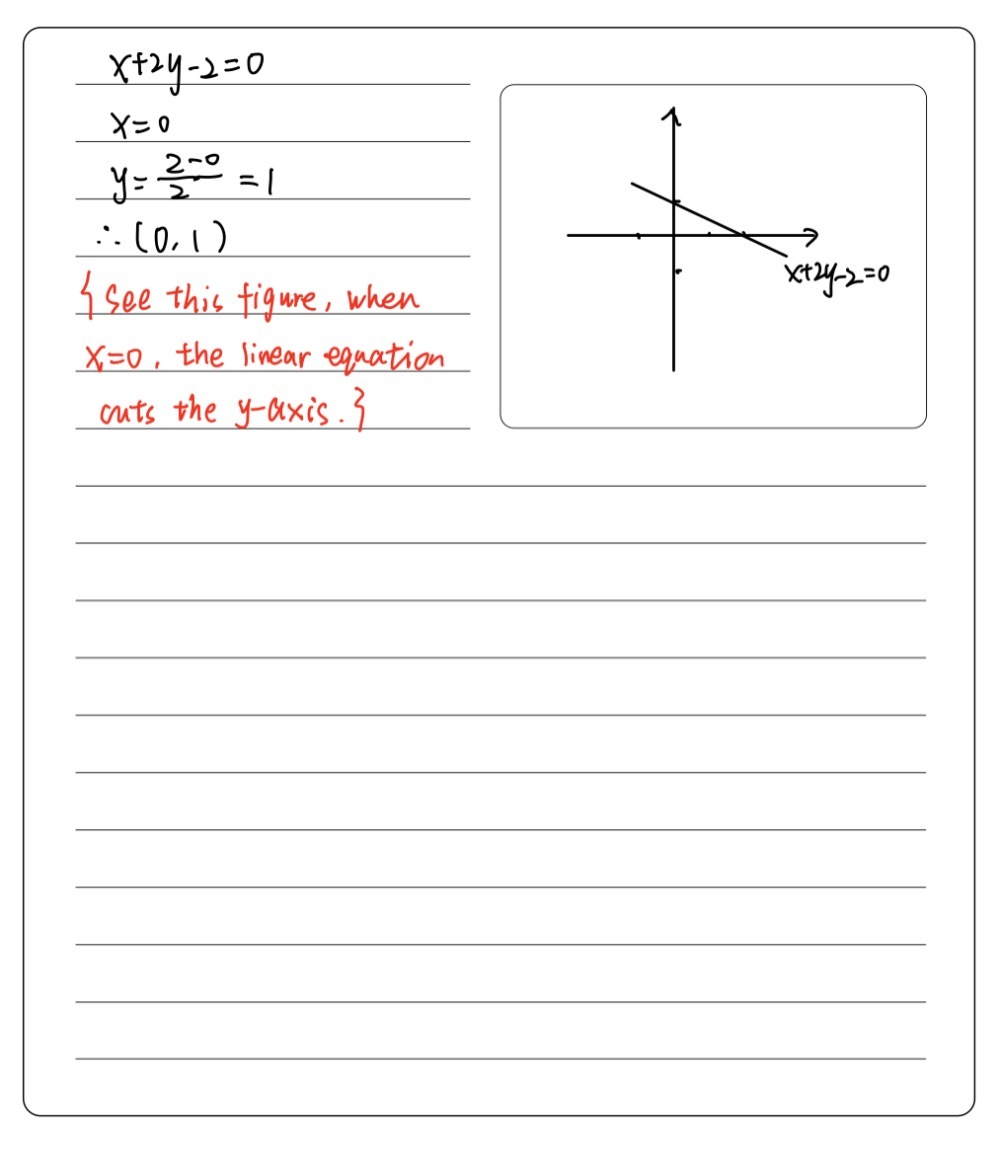



6 The Graph Of Linearequation X 2y 2 Cuts The Y Gauthmath



Find The Equation Of Tangent To The Curve Y X 7 X 2 5x 6 At The Point Where It Cuts The X Axis Sarthaks Econnect Largest Online Education Community
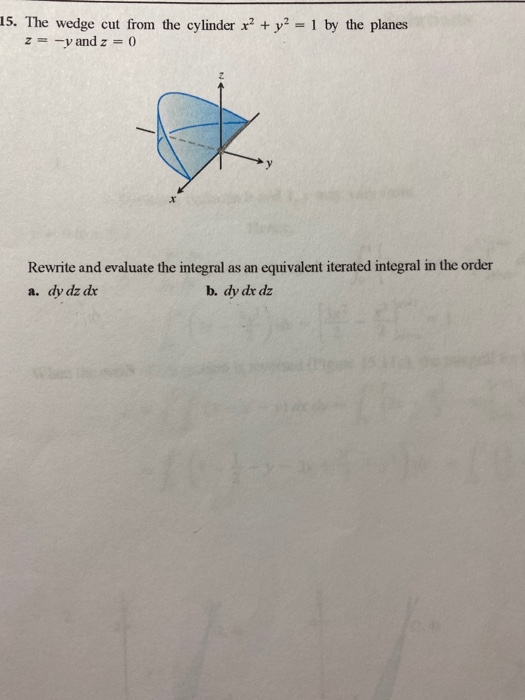



15 The Wedge Cut From The Cylinder X2 Y2 1 By Chegg Com




Draw The Graph Of The Equation 2x Y 6 Find The Coordinate Of The Point Where The Graph Cuts X Axis Brainly In




2 1 The Graph Below Cuts The X Exis At X 2 And X 2 Gauthmath




The Graph Of Linear Equation X 2y 2 Cut The Y Axis At Which Coordinate Brainly In




Calculus Volume Integral Mathematics Stack Exchange
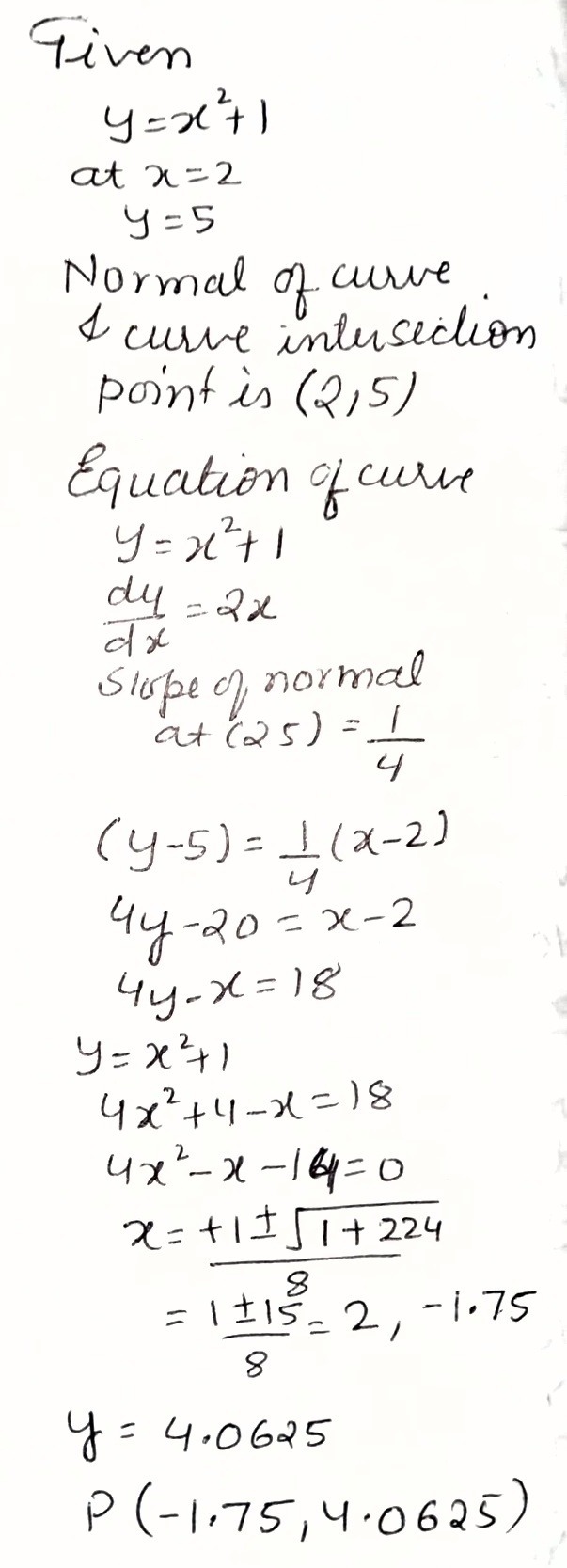



The Normal To The Curve Y X2 1 At The Point Where Gauthmath
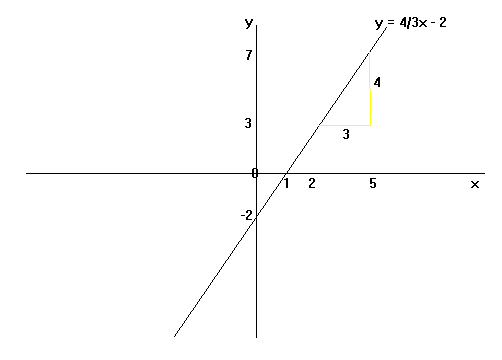



Equation Of A Straight Line Maths Gcse Revision




The Straight Line Y X 2 Rotates About A Point Where It Cuts



View Question A Polynomial Curve Have Turning Points At X 3 And X 2 It Cut S The Y Axis At 10 Find A Possible Equation Of The Curve




The Plane X 2y Z 4 Cuts The Sphere X 2 Y 2 Z 2 X Z 2 0 In A Ci
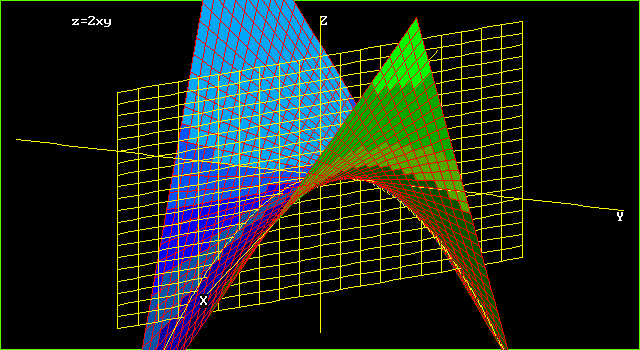



Graphs Of Surfaces Z F X Y Contour Curves Continuity And Limits




Differentiation F X X 3 2x 2 3x 5 F X 3x 2 4x 3 F 1 3 X X 1 3 3 4 If F X X 3 2x 2 Ppt Download




What Will Be The Equation Of The Circle Which Passes Through Origin 0 0 Has Its Centre On X Y 4 And Cuts Orthogonally The Circle X 2 Y 2 4x 2y 4 0 Quora
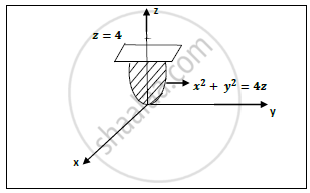



Find The Volume Of The Paraboloid X 2 Y 2 4 Z Cut Off By The Plane 𝒛 𝟒 Applied Mathematics 2 Shaalaa Com




Consider The Wedge Cut From The Cylinder X 2 Y 2 Chegg Com




If The Circle X 2 Y 2 A 2 Cuts Off A Chord Of Length 2b Fr




How To Find The Volume Of The First Octant Section Cut From The Region Inside The Cylinder Math X 2 Z 2 1 Math By The Planes Math Y 0 Z 0 X Y Math Quora



1
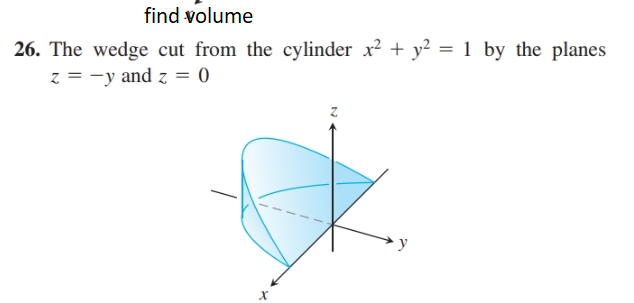



Answered Find Volume 26 The Wedge Cut From The Bartleby




Find The Points Where The Graph Of The Equation 3x 4y 12 Cuts The X Axis And Y Axis Brainly In




The Line Y X 2 Cuts The Parabola Y 2 8x In The Points A



Q Tbn And9gcsgtpqixxsgrkzlgw4sncpa Bzasa4aha6ydskojz1xbo 0yi Usqp Cau



Solved The Straight Line Y X 4 Cuts The Circle X 2 Y 2 26 At P And Q A Calculate The Coordinates Of P And Q B Sketch The Circle And T Course Hero




Find Equation Of Tangent To Y X 3 1 X 2 Find Interval Where
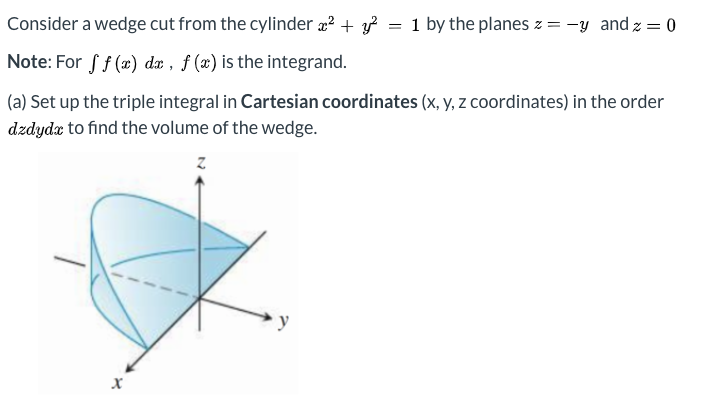



Consider A Wedge Cut From The Cylinder X2 Y2 1 By Chegg Com




Find The Coordinates Of The Point Where The Line Representing The Equation X 4 1 Y 6 Cuts The X Axis Brainly In




Slowness Curve For Sh 0 Wave In Lithium Niobate Y Cut Plate K X Download Scientific Diagram




Angelo Cuts A Piece Of Wood For A Project The First Cut Is Shown And Can Be Represented By The Brainly Com




Quadratic Graph Drawing Ppt Download




Show That The Circles X 2 Y 2 2x 6y 12 0 And X 2 Y 2 6x 4




The Graph Of Linear Equation X 2y 2 Cuts The Y Axis At Brainly In




If X Y Is A 2 Edge Cut Of A Graph G Every Cycle Of G That Contains X Must Also Contain Y Mathematics Stack Exchange



When Using Annotation As First Layer With X Discrete And Annotation Xmin Xmax Inf Inf Error Issue 3184 Tidyverse Ggplot2 Github



Find The Area Of The Smaller Part Of The Circle X 2 Y 2 A 2 Cut Off By The Line Sarthaks Econnect Largest Online Education Community




Equation To The Straight Line Cutting Off An Intercept 2 From Nega
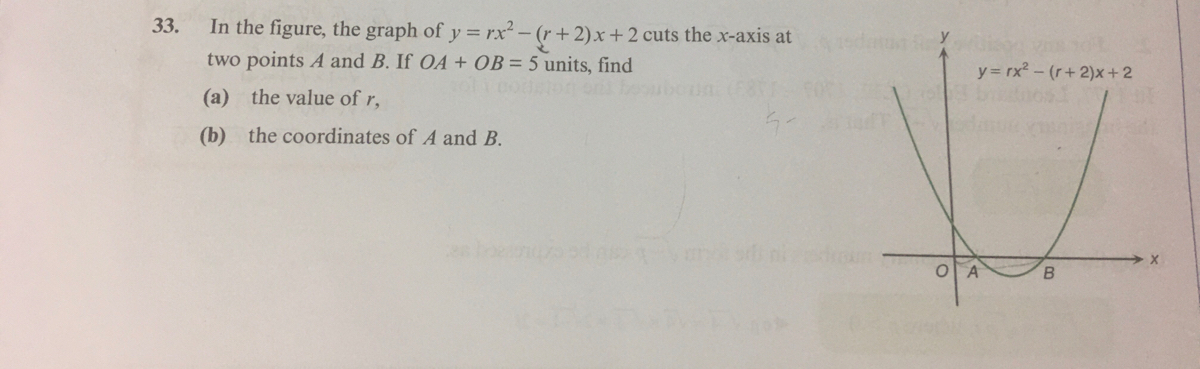



Answered In The Figure The Graph Of Y Rx Bartleby




A Variable Circle Cuts Each Of The Circles X 2 Y 2 2x 0 X 2 Y 2 4y 5 0 Orthogonally Youtube




Int Int B Int Dv Where B Is The Wedge Cut From The Cylinder X 2 Y 2 1 By The Planes Z 0 And Z Y Study Com




Cut Along The Y Axis At X L X 2 Of The Terms Of The Generalized Download Scientific Diagram




If X 2 A 2 Y 2 B 2 1 A B And X 2 Y 2 C 2 Cut At Right Angles




Graphs Of Surfaces Z F X Y Contour Curves Continuity And Limits
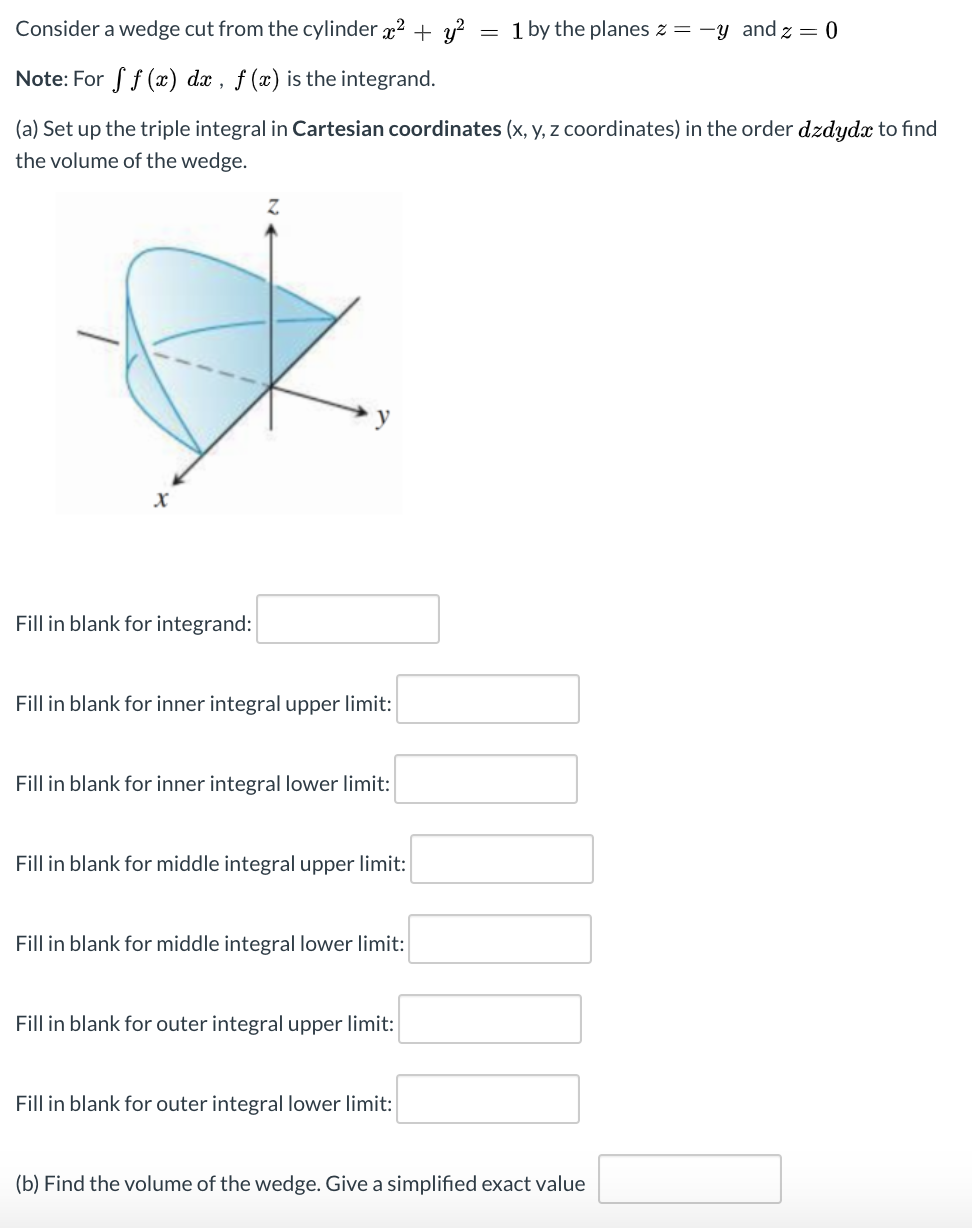



Solved Consider A Wedge Cut From The Cylinder X2 Y2 1 B Chegg Com




The Graph Of The Linear Equation 2x 3y 6 Cuts The Y Axis At The Po




L At What Point Straight Line Y X 2 1 2 Cuts Y Gauthmath



What Is The Distance Between Two Points If X Y 1 Cuts Circle X 2 Y 2 1 At Two Points Quora




Find The Volume Of The Region Cut From The Cylinder Chegg Com



Quadratic Function Parabola
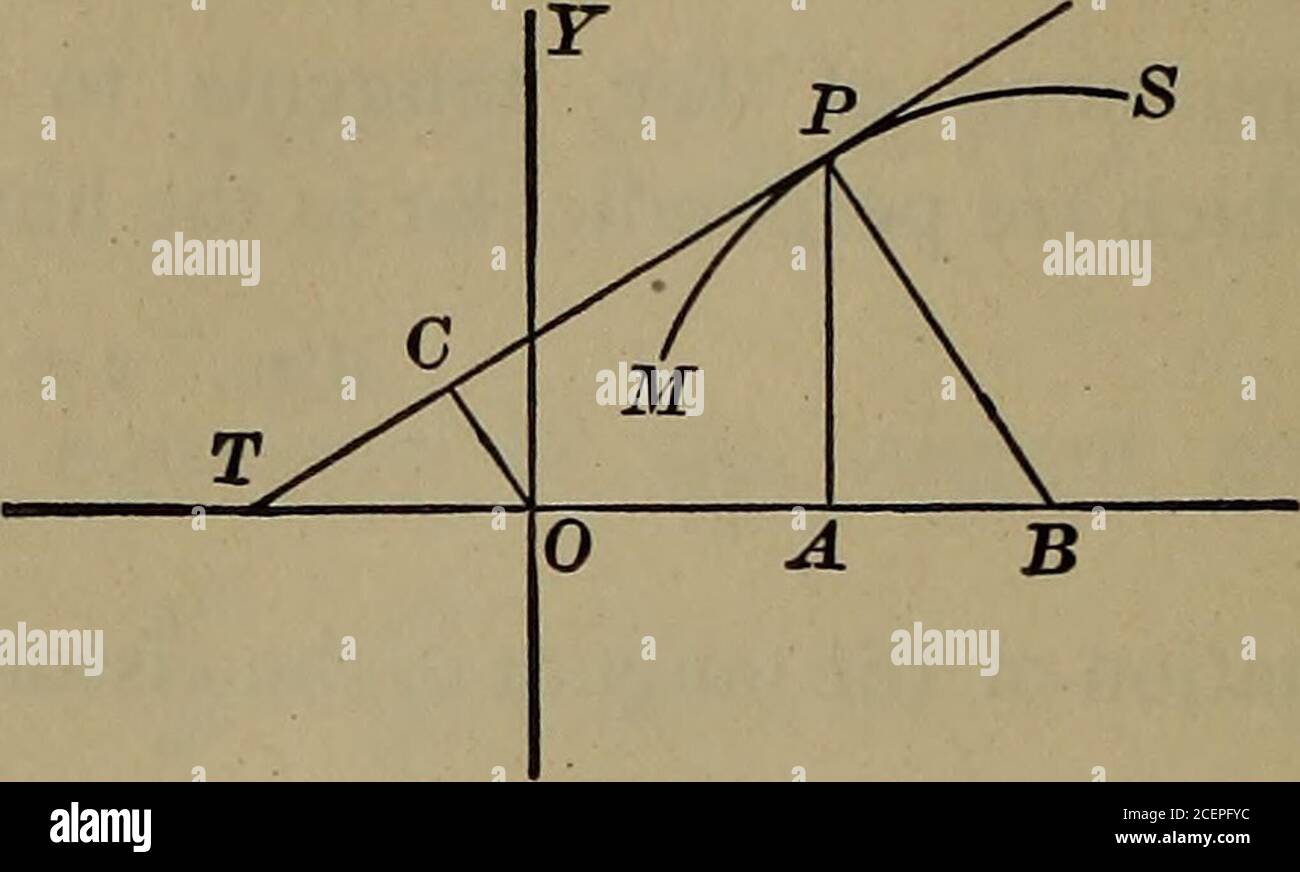



Differential And Integral Calculus To The Circle X 4 2 Y 3 2 25 At The Point 7 1 7 Find The Equations Of The Tangents To The Hyperbola4x2 Gy2 36




Evaluate The Volume Of The Solid Bounded By Z 8 X 2 Y 2 Z X 2 Y 2 X 1 Y Sqrt 3 X Y 0 Mathematics Stack Exchange




Ex 8 1 7 Find Area Of Smaller Part Of Circle X2 Y2 Cutoff
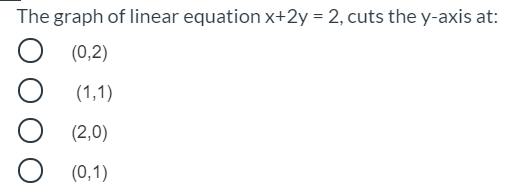



Answered The Graph Of Linear Equation X 2y 2 Bartleby




The Graph Of The Linear Equation 2x 3y 6 Cuts The Y Axis At The Point Youtube



Draw The Graph Of The Linear Equation 3x 4y 6 At What Points Does The Graph Cut The X Axis And The Y Axis Studyrankersonline




The Figure Shows The Curve Y See How To Solve It At Qanda




Type Ii Ncpm Wavelength For Shg In Y Cut Gd X Y 1 X Cob Versus X At Download Scientific Diagram



If A Line Y 3 X Cuts The Curve X 3 Y 3 3xy 5x 2 3y 2 4x 5y 1 0 At The Points A B And C



0 件のコメント:
コメントを投稿