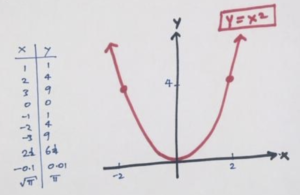
Answer to Consider the parabola y = 4x x^2 Graph the parabola and the tangent line to the parabola at the point (1, 3) By signing up, you'llFind the Focus y=x^212x Rewrite the equation in Tap for more steps Use the form , to find the values of , , and Consider the vertex form of a parabola Substitute the values of and into the formula Simplify the The focus of a parabola can be found by adding to the ycoordinate if the parabola opens up or down Substitute the Solve this 10 Consider the parabola y=x2 The shaded area is 1 232 533 734 Physics Motion In A Straight Line
Quadratic Graph Example Y Ax Expii
Consider the parabola y=x^2/4
Consider the parabola y=x^2/4-Calculus Algebra Mathematics Consider a parabola y = x 2 The line that goes through the point (0, 3/2) and is orthogonal to a tangent line to the part of parabola y = x 2Answer to Consider the following parabola y = 7x x^2 Find the slope of the tangent line to the parabola at the point (1, 6) By signing up,




How To Graph A Parabola 13 Steps With Pictures Wikihow
When we have the equation of a parabola, in the form y = ax^2 bx c, we can always find the x coordinate of the vertex by using the formula x = b/2a So we just plug in the values In this case, the equation in form y = ax^2 bx c is equal to y=x^2 4x 12Question Consider the parabola y=x^26x5 (i) Complete the square (ii) Give the Vertex (iii) Give the x and yintercepts (iv) Graph the parabola I have been working on this one but cannot get it rightIf so does it increase faster or slower than the x?
Parabola is a Ushaped plane curve where any point is at an equal distance from a fixed point and from a fixed straight line Click to learn more about parabola and its concepts Also, download the parabola PDF lesson for free Consider a parabola P that is congruent (has the same shape) to y=x^2 , opens upward, and has vertex (2,3) Now find the equation of a new parabola that results if P is Compressed to a factor of 1/2 Translated 2 units to the left Translated 3 units up Reflected in the xaxis and translated 2 units to the right and 4 units downConsider the parabola y = x^2 A) Show that the line through (3, 7) with the slope 2 is tangent to the parabola B) Find another line through (3, 7) that is tangent to the parabola Studycom
Would appreciate your help! 14) Consider the parabola with equation y = x^2 6x 5 a Use any suitable method to determine the coordinates of the turning point of this parabola b Hence, state for which values of c the line y = c will intersect the parabola i twice ii once iii not at all It is a standard horizontal parabola, the formula being y^2 = ax The focus point is formula a = 4p I know that Math PreCalc find the intersection between parabola y=x^2 3x 4 and line y=5x 11 math Consider the parabola y = 6x − x2



Parabolas And Cubics




Consider The Parabola Y X 2 7x 2 And The Straight Line Y 3x 3 The Equation Youtube
Math you own 5 pair of jeans and want to take 2 of them with you on vacation in how many ways can you choose 2 pairs of jeans A10 ways B15 ways C4 ways D ways NEED HELP!!Answered Consider the parabola y = x 2 4x – 3 bartleby Consider the parabola y = x 2 4x – 3 41 Find the coordinates of the focus * (A) (–2, –7) (B) (–9/4, –7) (–2, –27/4) (D) (–2, –29/4) 42 Find the equation of the directrix * (A) y = –27/4 (B) y = –29/4 y = –9/4 (D) y = –7/4 Consider the ellipse x^2/9y^2/4=1 and the parabola y^2 = 2x They intersect at P and Q In the first andfourth quadrants respectively Tangents to the ellipse at P and Q intersect the xaxis at R and tangents to the parabola at P and Q intersect the xaxis at S The ratio of the areas of the triangles PQS and PQR, is



8 Consider The Parabola Whose Equation Is Y X2 Gauthmath



Solution Find The Coordinates Of The Points Of Intersection Of The Parabola Y X2 And The Line Y X 2
Consider the basic upward parabola y=x^2 In this parabola as the x increases toward positive infinity , does the y value also increase toward infinity?Perimeter Let P(x, y) be a point on the parabola y = x 2 in the first quadrant Consider the triangle Δ P A O formed by P, A (0, 1), and the origin O (0, 0), and the triangle Δ P B O formed by P, B (1, 0), and the origin (see figure) (a) Write the area of each triangle in terms of xT = ³ 2 and when (x;



Graphing Quadratic Functions



1
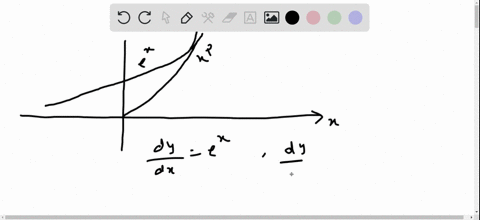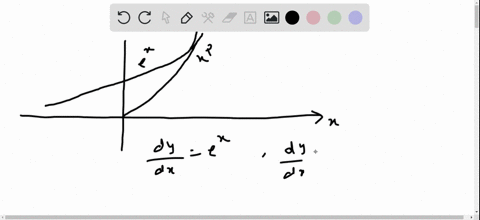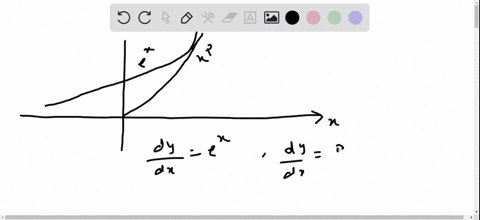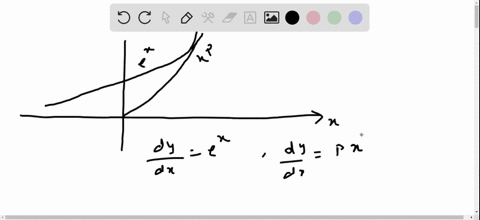
Consider the parabola y=x^{2} Let P, Q, and R be points on the parabola with R between P and Q on the curve Let \ell_{P}, \ell_{Q}, and \ell_{R} be the lineY) = (³ 2;Consider the parabola `y=x^(2)7x2` and the straight line `y=3x3` The equation `2x^(2)3y^(2)6=0` represents Consider the parabola `y=x^(2)7x2` and the straight line `y=3x3




Quadratic Functions Functions Siyavula




Consider Two Parabola Yx2 X1 See How To Solve It At Qanda
Consider the parabola y = x 2 Let P, Q, and R be points on the parabola with R between P and Q on the curve Let ℓ P, ℓ Q, and ℓ R be the lines tangent to the parabola at Consider the parabola y = x 2 ³ 6 Let x = t Then the parabola can be described by (x;Let (h,k)be the point closest to the line So, the tangent at (h,k)must be parallel to the given line y=x27x2 ∴dxdy =2x7 Slope of line y=3x−3is 3 ∴2h7=3 ∴h=−2 ∴k=h27h2=4−142=−8 Distance of point (−2,−8)from the line =∣∣∣∣∣∣ 32(−1)2 3(−2)−(−8)−3 ∣∣∣∣∣∣ =1 01




Characteristics Of Parabolas College Algebra




Consider The Parabola Y X 2 The Shaded Area Is Brainly In
Consider the parabola , let P and Q be two points and on the parabola Let R be a moving point on the arc of the parabola whose xcoordinate is between P and Q If the maximum area of triangle PQR is K, then is equal to 99k 1993k 416 Consider the parabola and the point F(0,1) let 7633The normal at P, Q, R on the parabola y 2 = 4 a x meet in a point on the line y = k then sides of the triangle PQR touch the parabola x 2 − 2 k y = 0 View solution Set of values of α for which the point ( α , 1 ) lies inside the curves c 1 x 2 y 2 − 4 = 0 and c 2 y 2 = 4 x isY=_____ I dont get what it is asking Please help!




Consider The Parabola P Touching X Axis At 1 0 And Y Axis 0 2 Directrix Of Parabola Youtube



Solved Examine These Quadratic Graphs The Black Parabola Is The Parent Function Y X 2 Which Is Actually In The Vertex Form Of A Quadratic Equ Course Hero
Answer to Consider the parabola y = 4x x^2 Find an equation of the tangent line to the parabola at point (1, 3) By signing up, you'll get I will consider the effect of small changes to the equation and then sketch my curve All of the following graphs have the same size and shape as the above curve I am just moving that curve around to show you how it works Example 2 y = x 2 − 2 The only difference with the first graph that I drew (y = x 2) and this one (y = x 2 − 2Consider the circle C x 2 y 2 6y 4 = 0 and the parabola P y 2 = x Then (A) the number of common tangents to C and P is 3 (B) the number of common tangents to C and P is 2 x 2y 1 = 0 is one of the common tangents (D) x 2y 1 = 0 is also one of the common tangents



Graphs Of Functions Y X2 Y 2x2 And Y 2x2 In Purple Red And Blue Respectively



Jduun1sdm Lxom
To get the area of the shaded region we use the concept of integration From the diagram, the limits of integration are x = 0 to x=2 Lets integrate the function We get x³ / 3 When we substitute the limits we get 2³/3 = 8/3 Area is thus 8/3 square units Consider the parabola y = x 2 Since all parabolas are similar, this simple case represents all others Construction and definitions The point E is an arbitrary point on the parabola The focus is F, the vertex is A (the origin), and the line FA is the axis of symmetry The line EC is parallel to the axis of symmetry and intersects the x axis at D9 Find the area of the region bounded by the parabola y = x^2 and y= xarea of region bounded,area of a bounded region,area of the region bounded by the gr




Solved Consider The Parabola Y X X 2 And The Inscribed Chegg Com
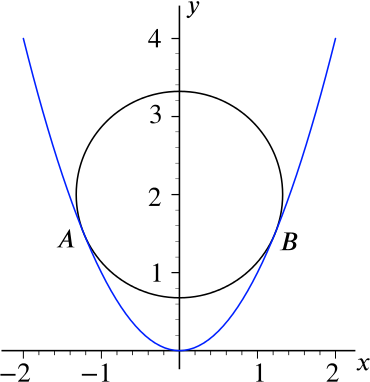



Solution When Does A Circle Touch A Parabola Twice Circles Underground Mathematics
Consider the parabola y=x^2 A particle starts from the origin and travels along the parabola into the first quadrant so that its distance from the origin is increasing at the constant rate of 2 m/s The path of the particle follows the curve of the parabola The normal line passing through the particle intersects the positive yaxisExploring Parabolas by Kristina Dunbar, UGA Explorations of the graph y = ax 2 bx c In this exercise, we will be exploring parabolic graphs of the form y = ax 2 bx c, where a, b, and c are rational numbers In particular, we will examine what happens to the graph as we fix 2 of the values for a, b, or c, and vary the third We have split it up into three partsE = − 2 e = 2 Substitute the values of a a, d d, and e e into the vertex form a ( x d) 2 e a ( x d) 2 e ( x 0) 2 − 2 ( x 0) 2 2 ( x 0) 2 − 2 ( x 0) 2 2 Set y y equal to the new right side y = ( x 0) 2 − 2 y = ( x 0) 2 2 y = ( x 0) 2 − 2 y = ( x 0) 2 2




Parabola Wikipedia



Investigating Parabolas International Baccalaureate Maths Marked By Teachers Com
Consider the parabola y^2 = 8x Let Δ1 be the area of the triangle formed by the end points of its latus rectum and the point P (1/2,2) on the parabola, and Δ2 be the area of the triangle formed by drawing tangents at P and at the end points of the latus rectum Then Δ1/Δ2 isConsider the region bounded by the line y = 2x and the parabola y = x^2 Set up, but do not evaluate the integral (or integrals) you would use to find the volume of the solid obtained by revolving this region about the xaxis Consider the region bounded by the parabola y = xConsider the parabola y = x^2 The shaded area is Consider the parabola y = x




Consider The Parabola Whose Equation Is Y X 2 4x And The L
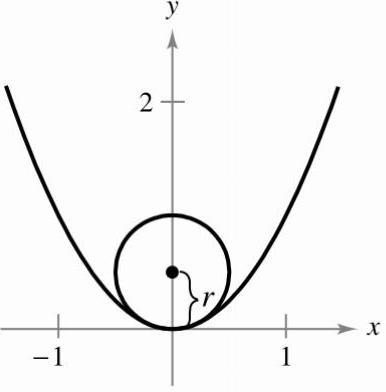



Consider The Graph Of The Parabola Y X 2 1 Find The Radius R Of The Largest Possible Circle Centered On The Y Axis That Is Tangent To The Parabola At The Origin As Shown In The
Consider a hyperbola H `x^ (2)y^ (2)` =k and a parabola `Py=x^ (2)` then identify the Consider a hyperbola H `x^ (2)y^ (2)` =k and a parabola `Py=x^ (2)` then identifyConsider the parabola y = 8x x2 Find the slope of the tangent line to the parabola at the point (1, 7) Find an equation of the tangent line In part (a) y = Graph the parabola and the tangent lineConsider the parabola y = 4x − x2 (a) Find the slope of the tangent line to the parabola at the point (1, 3) (b) Find an equation of the tangent line in part (a) y = (c) Graph the parabola and the tangent line Question Consider the parabola y = 4x − x2 (a) Find the slope of the tangent line to the parabola at the point (1, 3)




Consider Three Points Ppt Download




A Parabola Y X 2 Is Parametrised By X T And Y T 2 A Point P Lies On The Normal To The Parabola At A T T 2 And Ap Is 1 Unit In Length Find The Equation Of
Consider the parabola y=6xx^2 Show transcribed image text Expert Answer 100% (6 ratings) Previous question Next question Transcribed Image Text from this Question Consider the parabola y = 6x x^2 Find the slope of the tangent line to the parabola at the point (1, 5) ____ Find an equation of the tangent line in part (a)Finding Equations of Circles Consider the graph of the parabola y = x 2 (a) Find the radius r of the largest possible circle centered on the y axis that is tangent to the parabola at the origin, as shown in the figureThis circle is called the circle of curvature (see Section 125) Find the equation of This makes sense if we consider the fact that the vertex, in this case, is the lowest point on the graph and so the graph simply can't touch the \(x\)axis anywhere else The fact that this parabola has only one \(x\)intercept can be verified by solving as we've done in the other examples to this point
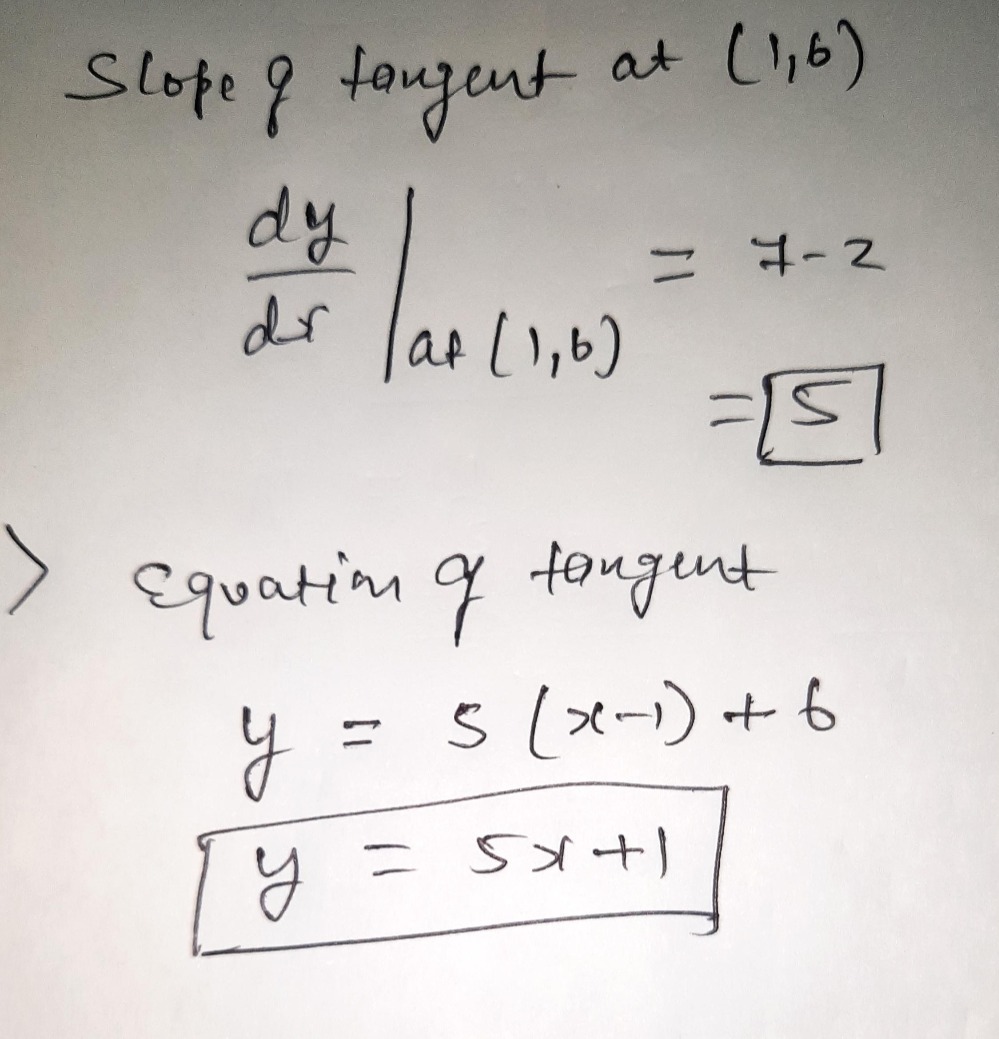



Consider The Parabola Y 7x X2 A Find The Slope Of Gauthmath



Solved Consider The Parabola Y X 2 Let P Q
Answer to Consider the parabola y = 4x x^2 Find the slope of the tangent line to the parabola at the point (1, 3) By signing up, you'll getT = 3 Thus aFind the Vertex Form y=x^210x16 Complete the square for Consider the vertex form of a parabola Substitute the values of and into the formula Cancel the common factor of and



Solved Consider The Parabola Y 4x X2 A Find The Slope M Of The Tangent Line To The Parabola At The Point 1 3 I Using This Denition The Course Hero
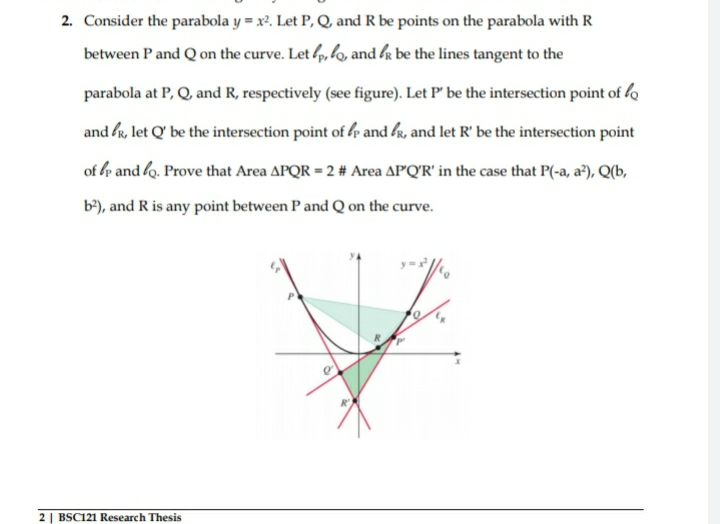



2 Consider The Parabola Y X2 Let P Q And R Be Chegg Com
T 2 ³ 6) Now when (x;Yes, faster, it increases as the square of xFirst question Find the value of c such that y=x c is a tangent to the parabola y=x 2 x12 (Hint Consider the discriminant of the resulting quadratic) Second question Find the values of m for which the straight line y= m x6 is tangent to the parabola y=2x 2 6x2
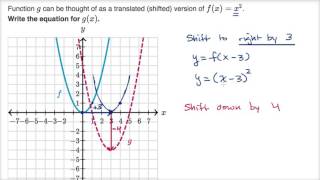



Shifting Parabolas Video Khan Academy




How To Graph A Parabola 13 Steps With Pictures Wikihow
The parabola y=x^2 is scaled vertically by a factor of 1/10 What is the equation of the new parabola?Finding Equations of Circles Consider the graph of the parabola y = x 2 (a) Find the radius r of the largest possible circle centered on the yaxis that is tangent to the parabola at the origin, as shown in the figureThis circle is called the circle of curvature (see Section 125) Find the equation of this circle Use a graphing utility to graph the circle and parabola in the same viewingLet V be the vertex and L be the latus rectum of the parabola x 2 = 2 y 4 x − 4 Then the equation of the parabola whose vertex is at V , latus rectum is L / 2 and axis is perpendicular to the axis of the given parabola




Find The Point On The Parabola 2y X 2 That Is Closest To The Point 4 1 Mathematics Stack Exchange




B Examine The Graph Of T Descubre Como Resolverlo En Qanda
Free Parabola calculator Calculate parabola foci, vertices, axis and directrix stepbystep This website uses cookies to ensure you get the best experience parabolaequationcalculator y=x^{2}4 en Related Symbolab blog posts Practice, practice, practiceConsider the parabola `y=x^(2)7x2` and the straight line `y=3x3` The equation of the ellipse whose centre is at origin, major axis is along xaxis with Consider the parabola `y=x^(2)7x2` and the straight line `y=3x3




8 Consider The Parabola Whose Equation Is Y X2 Gauthmath



Consider A Parabola Math Y X 2 Math The Line That Goes Through The Point 0 3 2 And Is Orthogonal To A Tangent Line To The Part Of Parabola Math Y X 2 Math With Math X 0 Math Is Math Y Ax 3 2 Math What
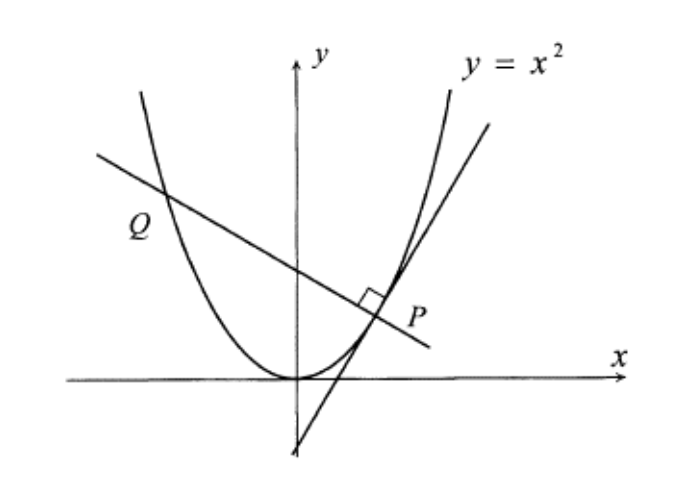



Solved Consider The Parabola 𝑦 𝑥2 And Some Fixed Yet A Chegg Com



Further Pure 1 Chapter 2 Conics 1 Ppt Download
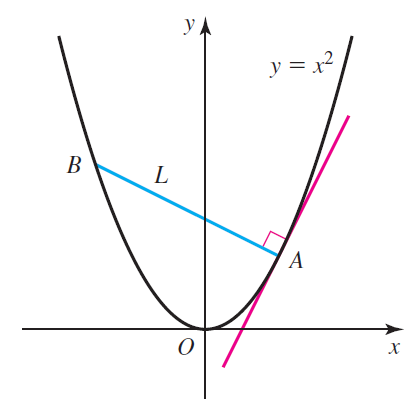



Solved Two People A And B Walk Along The Parabola Y X 2 In Such A Way Tha Solutioninn
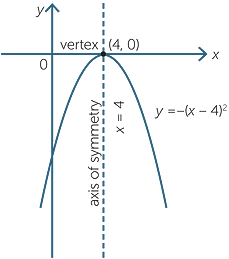



Quadratic Function



Ny Schoolwires Net Cms Lib Ny Centricity Domain 196 Algebra i Regents review Jmap worksheets A G 5 Stretchingquadraticfunctions Pdf



3 1 Some U Shaped Graphs G Day Math




Graph Of Y X 2 The Equation For A Parabola Download Scientific Diagram




Solve This 10 Consider The Parabola Y X2 The Shaded Area Is 1 232 533 734 Physics Motion In A Straight Line Meritnation Com
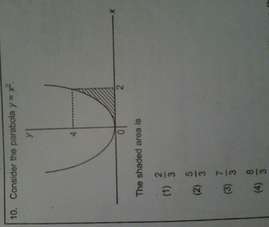



10 Consider The Parabola Yx 4 0 2 The Shaded Area Is 2 3 Scholr



Algebra Parabolas



Consider The Parabola Y 2 4x Let P And Q Be Points On The Parabola Where P 4 4 Q 9 6 Sarthaks Econnect Largest Online Education Community




Given The Graph Consider The Parabola H Y X 2 Let Gamma Be The Arc Of H From A 0 0 To B 1 1 Evaluate The Scalar Integral Int Gamma Sqrt Y Ds Study Com




Parabola Wikipedia
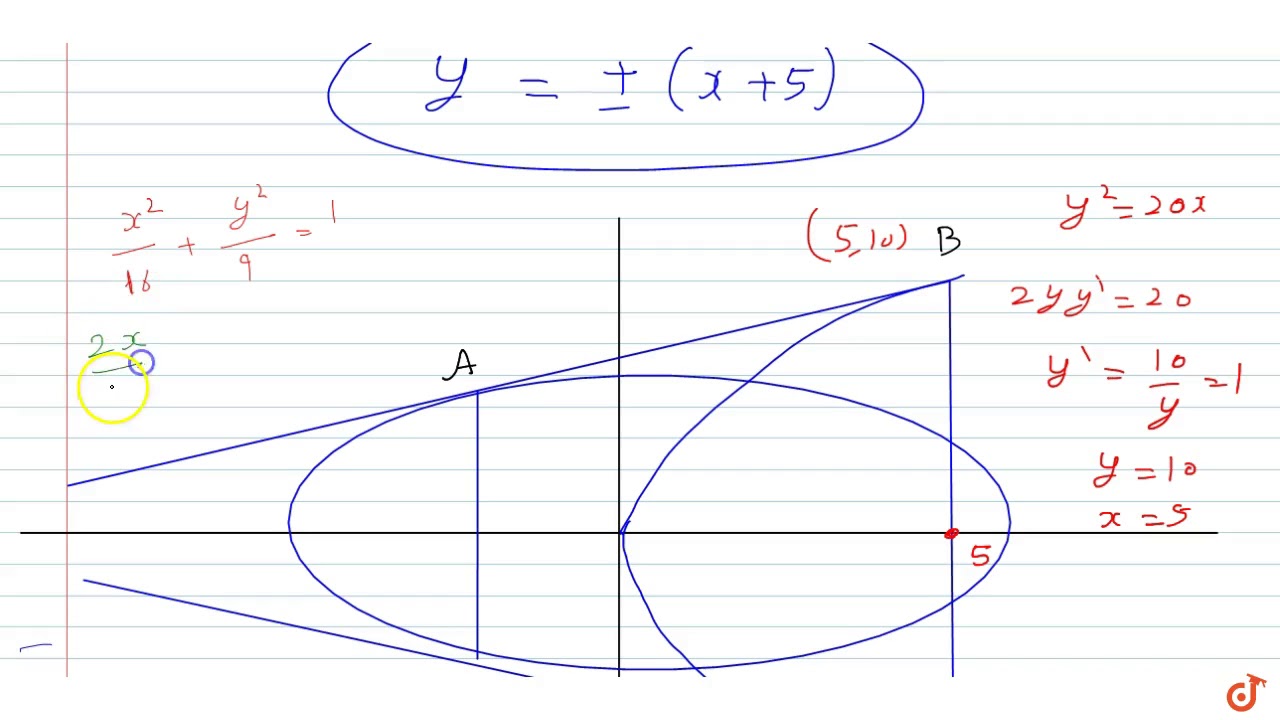



Consider The Parabola Y 2 x Ellipse X 2 16 Y 2 9 1 And Hyperbola X 2 29 Y 2 4 1 The E Youtube
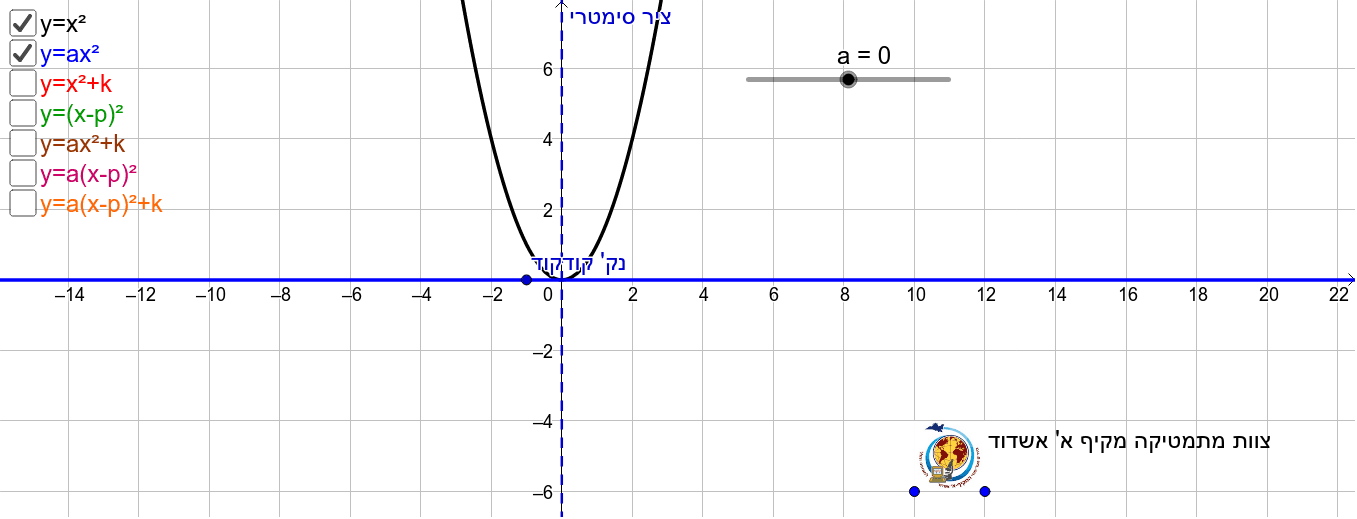



Parabola Y X 2 Geogebra



Quadratics Graphing Parabolas Sparknotes




Consider A Parabola P That Is Congruent To Y X 2 Opens Upward And Has Vertex 0 0 Find The Brainly Com



Solution Consider The Parabola Y X2 6x 4 What Is The Axis Of Symmetry X Compute The Coordinates Of The Vertex Compute The Y Intercept As A Point Find The Po
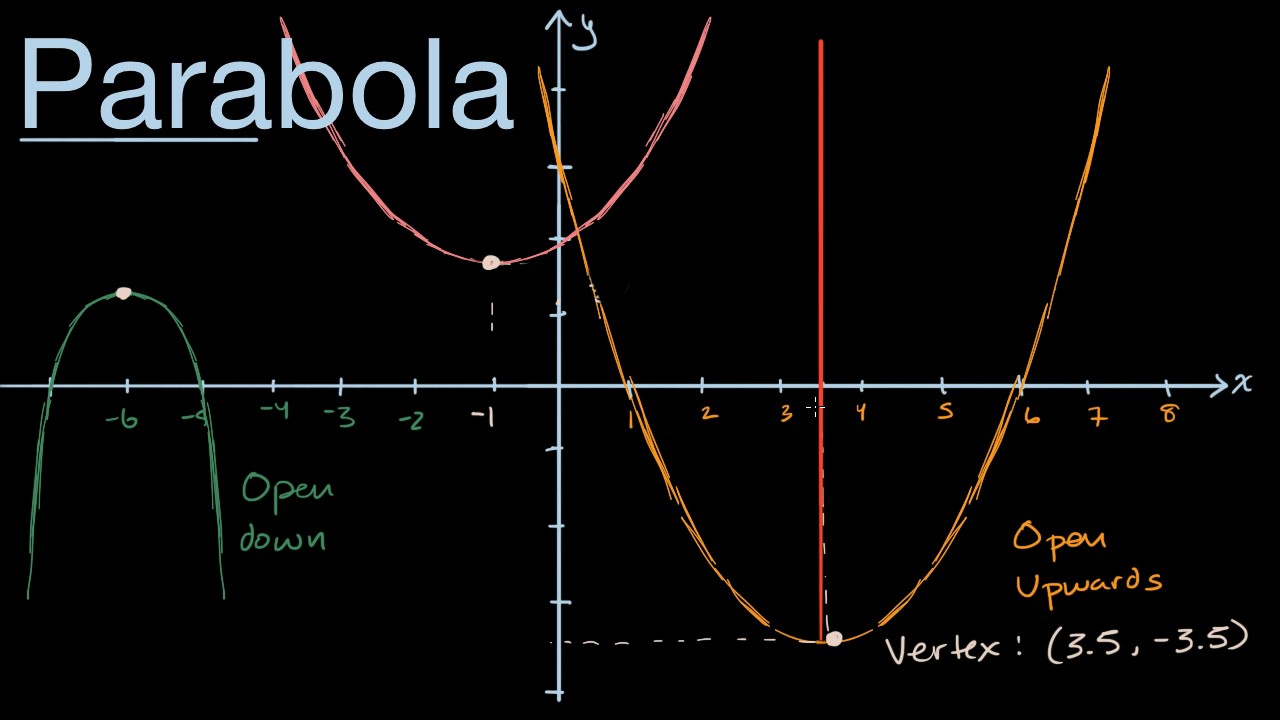



Parabolas Intro Video Intro To Parabolas Khan Academy




Consider The Parabola Y X 2 7x 2 And The Straight Line Y 3x 3
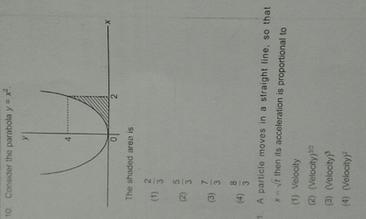



10 Consider The Parabola Y X 4 0 The Shaded Area Is 1 A Par Scholr
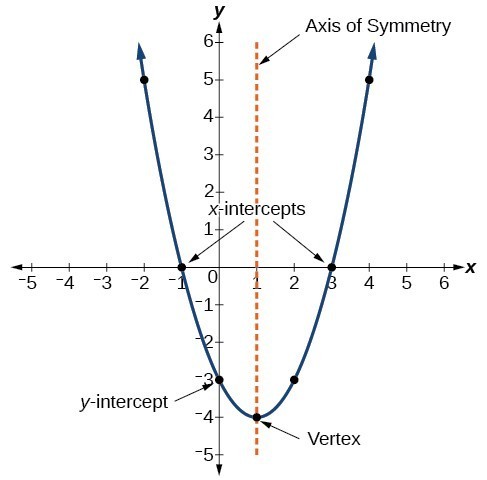



Characteristics Of Parabolas College Algebra




Solve This 10 Consider The Parabola Y X2 The Shaded Area Is 1 232 533 734 Physics Motion In A Straight Line Meritnation Com




Graph Of Y X 2 The Equation For A Parabola Download Scientific Diagram
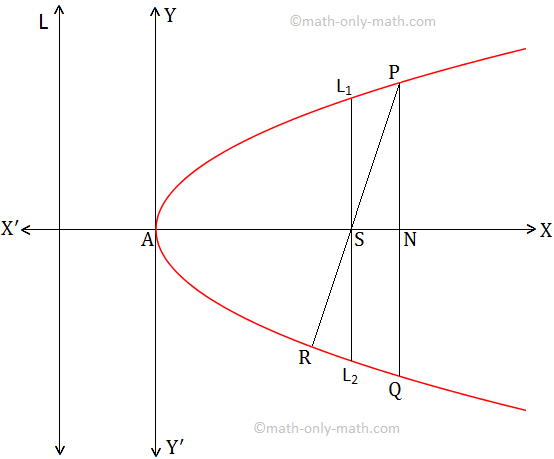



Concept Of Parabola Definition Of Parabola Directrix Of The Parabola




Find Consider The Parabola Y X 2 In Two Dimensions What Is The Torsion For This Parabola Thinking Problem Only No Calculations Study Com



Find The Point On The Parabola Y 2 2x That Is Closest To The Point 1 4 How Can I Approach This Quora



1




Ex 8 1 9 Class 12 Find Area Bounded By Parabola Y X 2 And Y X



Math Spoken Here Classes Quadratic Equations 3




Quadratic Graph Example Y Ax Expii




Consider Two Parabola Y X 2 X 1 And Y X 2 X 1 2 The Parabola Y




Consider The Parabola Y 2 8x Let D1 Be The Area Of The Triangle Formed By The End Points Of Its Latus Rectum And The Point P 1 2 2 On The Parabola



Parabola Equation




Ex 8 1 9 Class 12 Find Area Bounded By Parabola Y X 2 And Y X
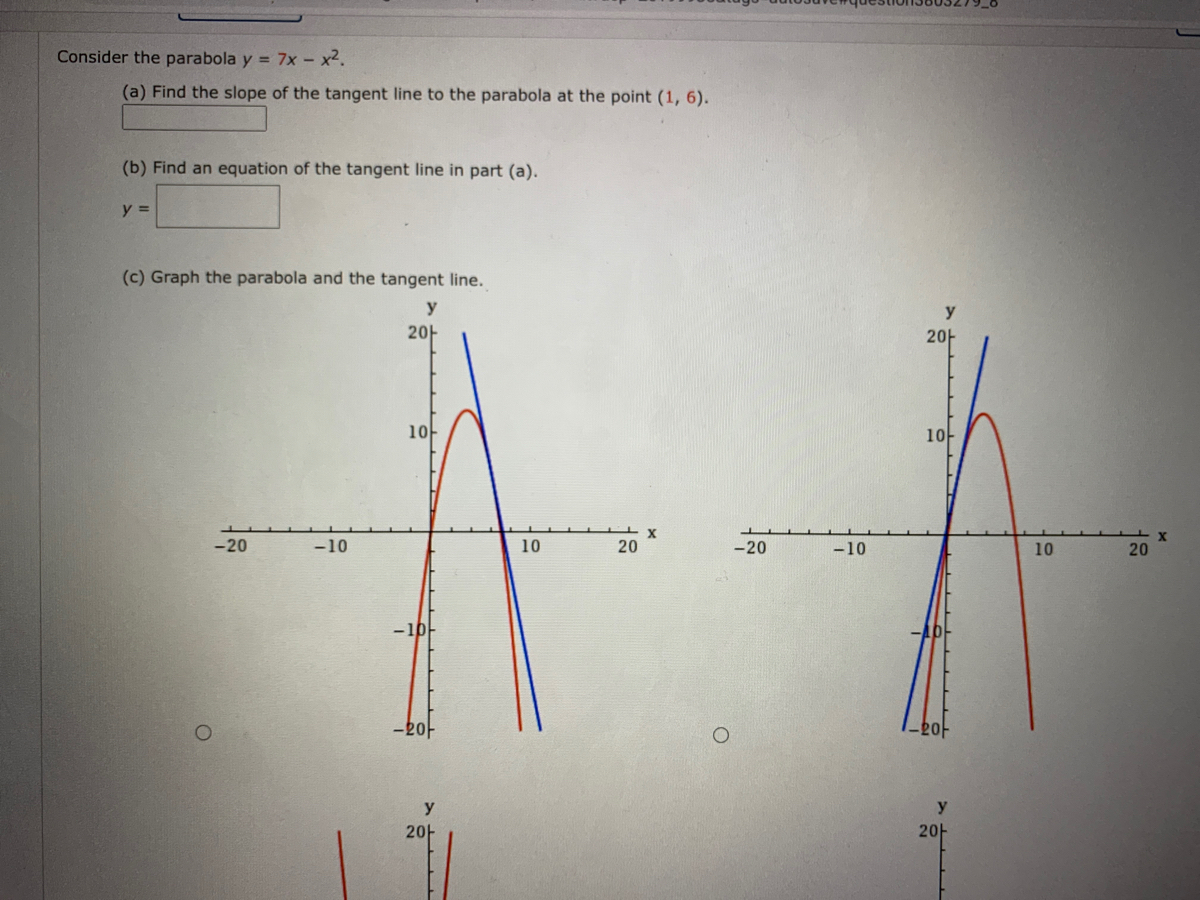



Answered Consider The Parabola Y 7x X2 A Bartleby




In The Given Parabola Y X2 Find The Area Of The Shaded Portion The Shaded Physics Motion In A Straight Line Meritnation Com
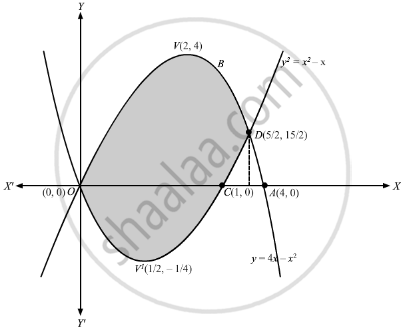



Find The Area Enclosed By The Parabolas Y 4x X2 And Y X2 X Mathematics Shaalaa Com



Biomath Quadratic Functions




Consider The Region Bounded By The Parabola Y X 2 And The Line Y 9 What Is The Volume Of The Solid Generated When Revolving This Region About The Line
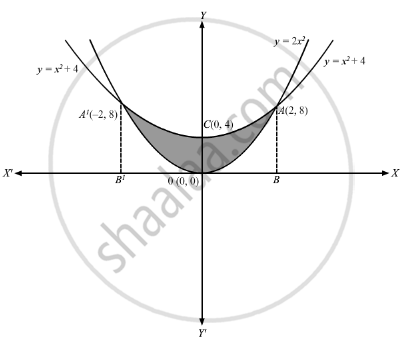



Prove That The Area Common To The Two Parabolas Y 2x2 And Y X2 4 Is 32 3 Sq Units Mathematics Shaalaa Com




How To Draw Y 2 X 2




19 Consider The Parabola Y X2 11 1 Solution The Shaded Area Is Win Wi 3
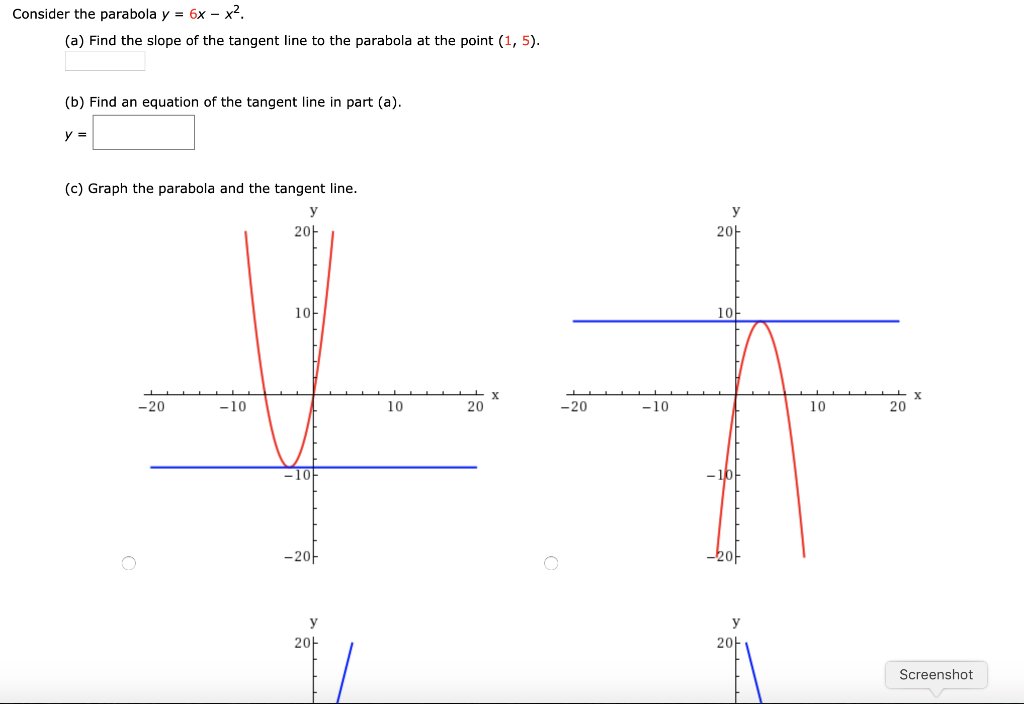



Consider The Parabola Y 6x X2 A Find The Slope Chegg Com



Let C1 And C2 Be Respectively The Parabolas X 2 Y 1 And Y 2 X 1 Let P Be Any Point On C1 And Q1 Be Any Point Sarthaks Econnect Largest Online Education Community




How Do You Graph Y X 2 1 Socratic
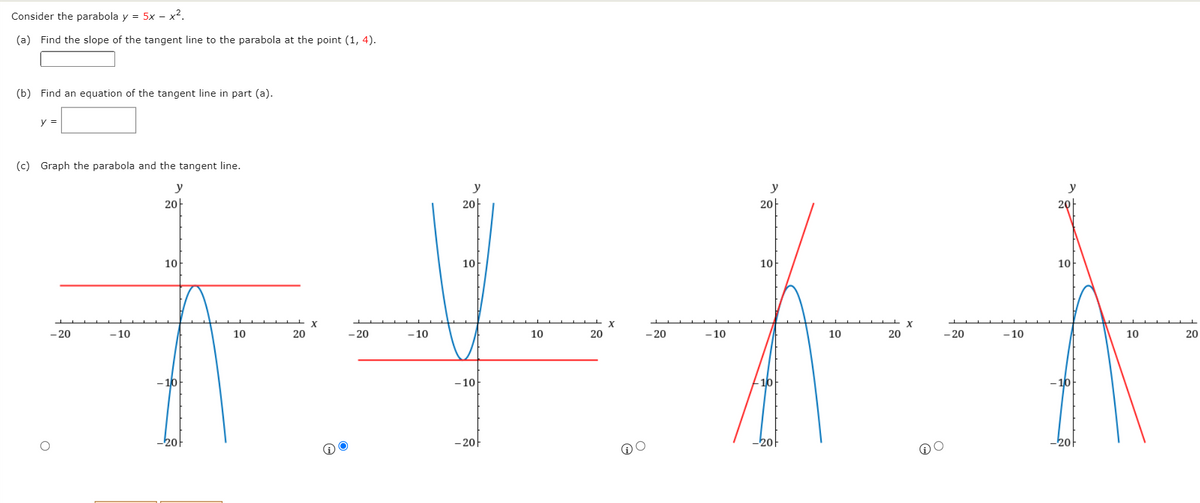



Answered Consider The Parabola Y 5x X2 A Bartleby




Pin On Quick Saves



How To Write The Vertex Of The Parabola Y X 2 8x 10 Quora




Find Area Of The Region Bounded By Parabola Y 2 8x And Line X 2



Curvature And Radius Of Curvature Page 2



Mfm2p



Www Ijser Org Researchpaper A Parabola Symmetrical To Y X Line Pdf




Quadratic Function
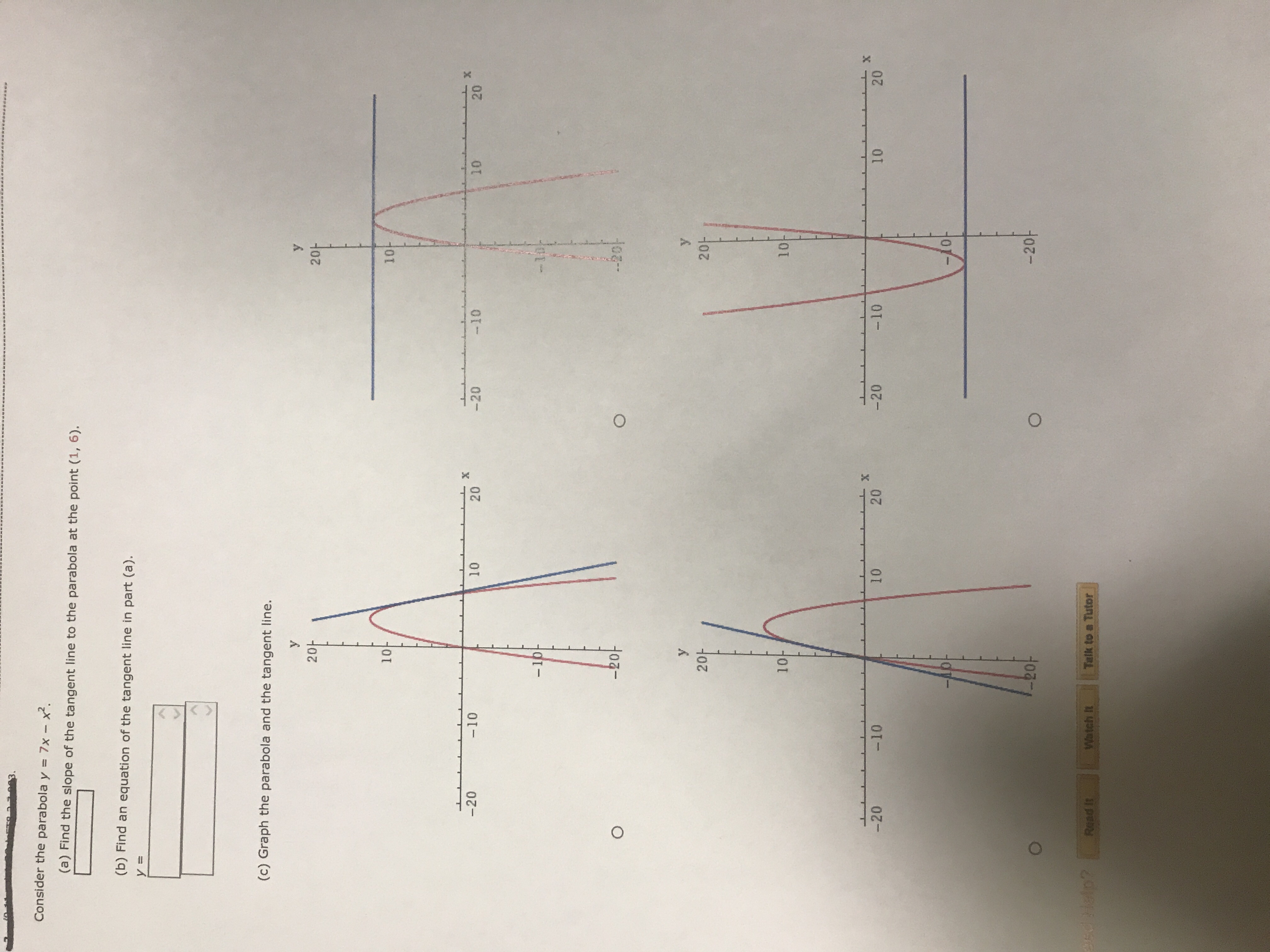



Answered Consider The Parabola Y 7x X Find The Bartleby




A Variable Chord Pq Of The Parabola Y X 2 Subtends A Right Angle At The Vertex Then The Locus Of Points Of Intersection Of The Normals At P Amp Q Is




How To Graph A Parabola 13 Steps With Pictures Wikihow
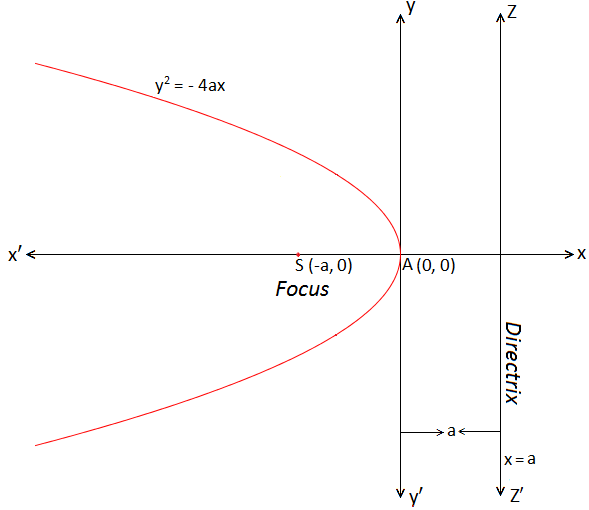



Standard Form Of Parabola Y 2 4ax Equation Of A Parabola Solved Examples




Quadratic Function




Consider The Parabola Y X 2 The Shaded Area Is
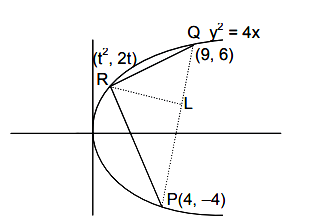



Consider The Parabola Y2 4x Let P And Q Be Points On The



1
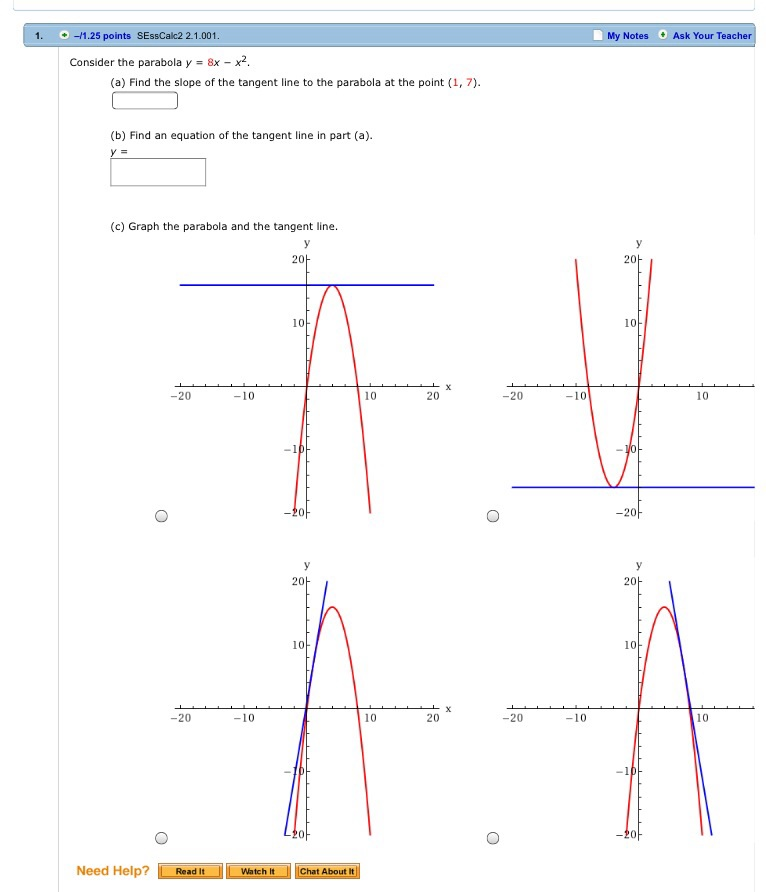



Consider The Parabola Y 8x X2 Find The Slope Of Chegg Com




Parametric Equations




Topological Variation For The Offsets Of The Parabola Y X 2 Download Scientific Diagram
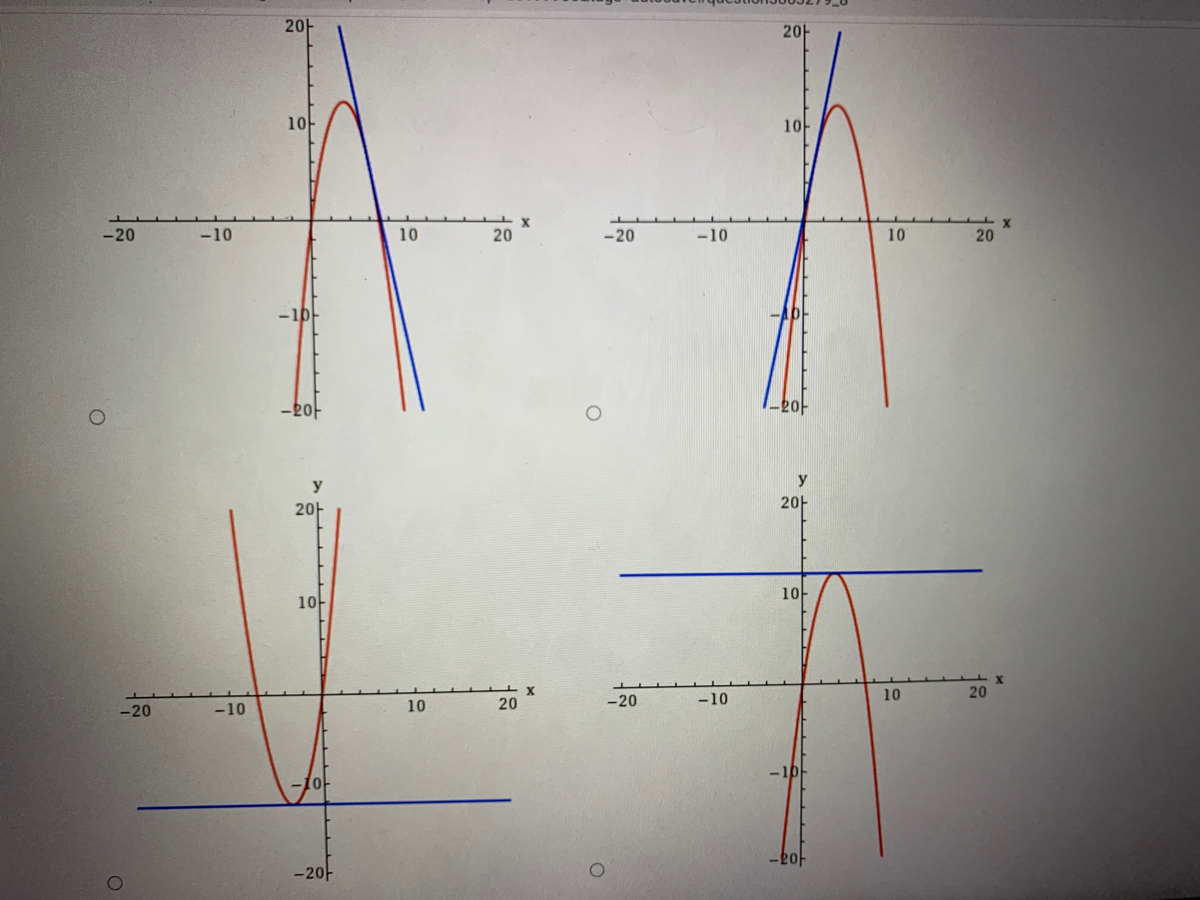



Answered Consider The Parabola Y 7x X2 A Bartleby




Consider The Parabola Y X 2 7x 2 And The Straight Line Y 3x 3
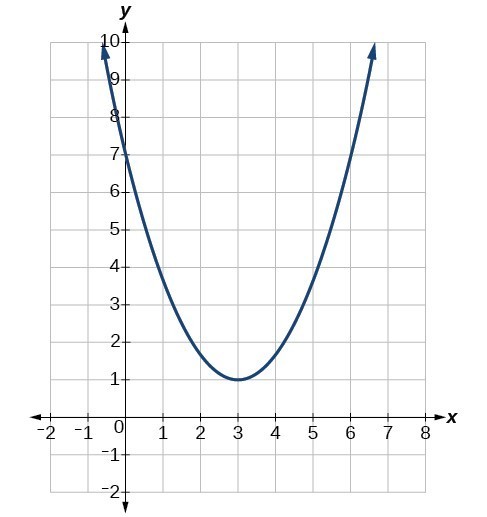



Characteristics Of Parabolas College Algebra
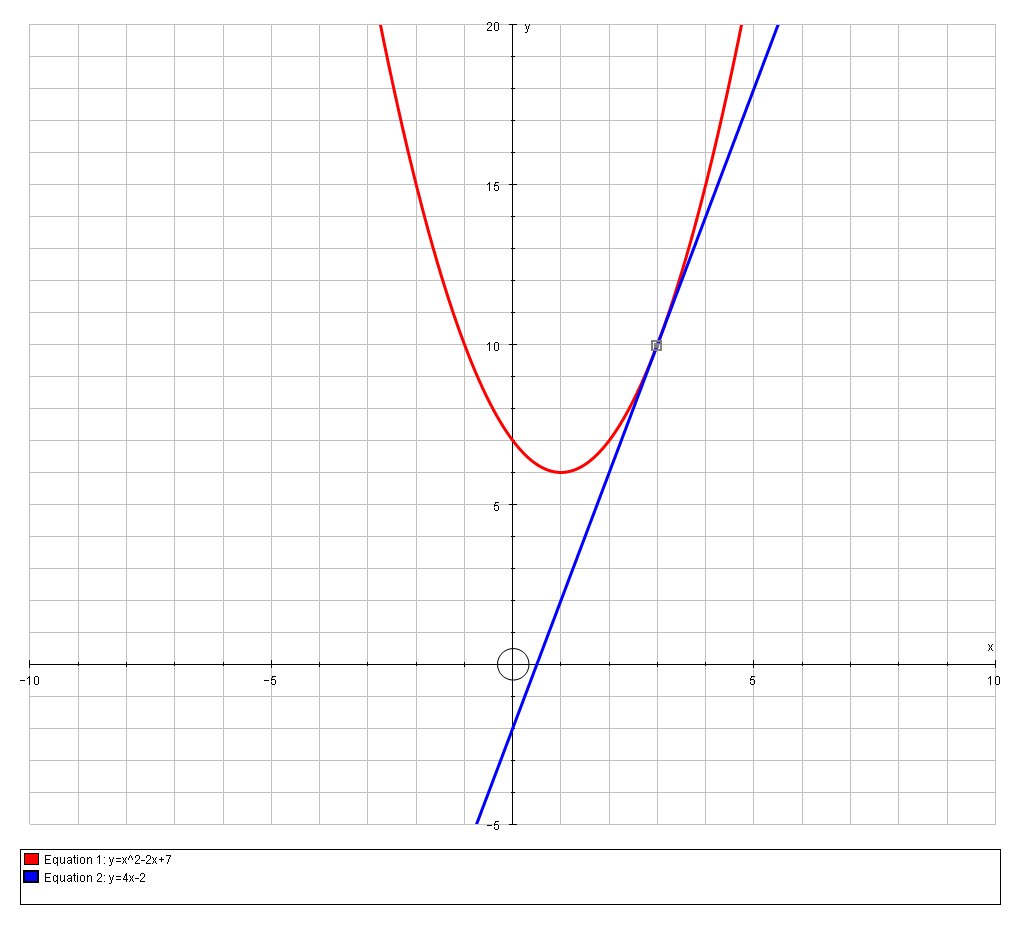



How Do You Find An Equation Of The Tangent Line To The Parabola Y X 2 2x 7 At The Point 3 10 Socratic
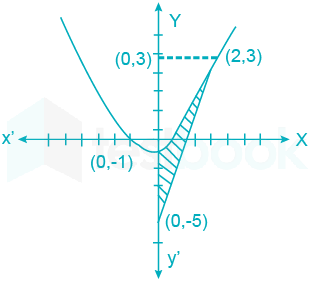



Solved The Area In Sq Units Bounded By The Parabola Y X 2 1 The Self Study 365
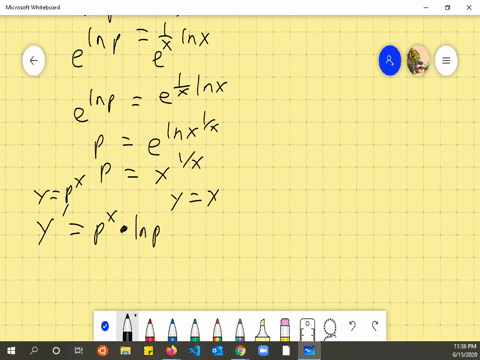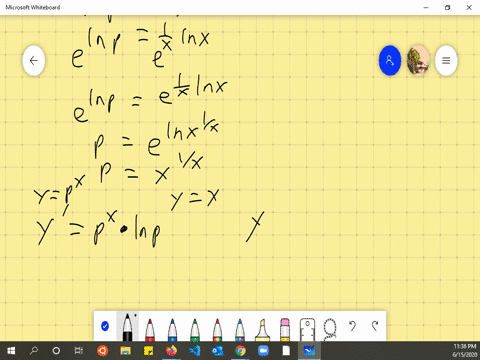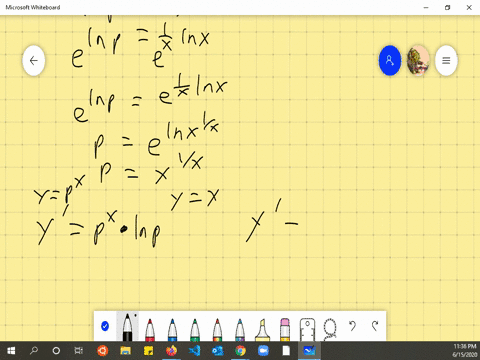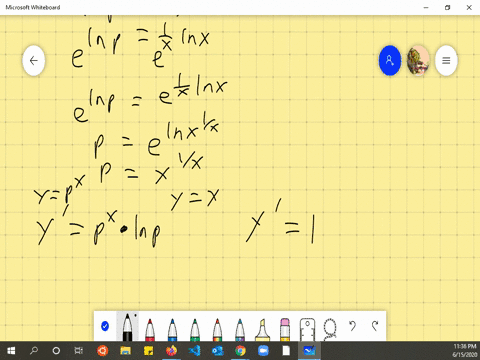



Solved Consider The Parabola Y X 2 Let P Q



Math Spoken Here Classes Quadratic Equations 3



0 件のコメント:
コメントを投稿