平面図形 面積と比 説明 Date09年 6月15日 三角形の面積について,次のことが成り立ちます。 1 高さが等しい三角形の面積は,その底辺の長さに比例する。 2 底辺の長さが等しい三角形の面積は,その高さに比例する。 を頂点 を通る直線 で と に分ける平面図形の面積(灘 07) 正五角形の面積(東海 04) 正三角形と正六角形 補助線の威力(灘 01) 平面図形の面積 (三田学園 1998 改題) SAPIX 6月マンスリー 算数問題(相似と比) 正方形の一辺の長さ(中学受験 算数問題 女子学院09) 正六角形の部分の面積(sapix補充算数プリントよ底辺×高さ÷2=面積 a×h 2 1 a h 台形の面積 (上底下底)×高さ÷2=面積 (ab )×h 2 1 h(ab ) 平行四辺形の面積 底辺×高さ=面積 a×h=a h ひし形の面積 対角線×対角線÷2=面積 a×b 2 1 a b 円の面積

いろいろな面積を求める問題1 中学受験準備のための学習ドリル
平面図形の面積 影の部分の面積
平面図形の面積 影の部分の面積- 平面図形「ひし形の面積は、一方の対角線×他方の対角線÷2、正方形の面積は、対角線×対角線÷2」 オンライン家庭教師はじめました。 ③ 上記ホームページ の下の方にに私宛のメッセージ機能(STEP1として「ワンセンテンス算数さんにメッセージを送る平面図形の面積 (A),周長 (L)および重心位置 (G) 単位換算 公式計算 データソート 技術データ集:掲載項目 掲載ページ 三角形 P11 平行四辺形 P11 台形 P11 四辺形 P11 正n角形 P11 円 P11 扇形 P11 弓形 P11 楕円 P11 放物形 P11



面積 これが中学入試に出た図形問題
平面図形 三角形の面積に関する基本的な問題です。 4年生向け 東京学芸大学附属世田谷中学校13 平面図形 4年生向け 京都学園中学校13 平面図形 フィードバック(不具合・誤記・問題解法の矛盾に関する連絡) 平面図形 面積 三角形 四角形 正方形 長方形 台形 平行四辺形 ひし形 平面図形の面積の求め方の公式 台形=(上底+下底)×高さ÷2 ひし形(対角線直交四角形)の面積=対角線×対角線÷2 円周=直径×円周率(314)=半径×2×円周率(314) 円の面積=半径×半径×円周率(314) おうぎ形の弧の長さ=円周×中心角/360=直径×314×中心角/360 おうぎ形の面積=円の面積×中心角/360=半径×半径×円周率×中心角/360 レンズ形の平面図形や形 親トピック 幾何 幾何 数学 平面図形 面積 円 多角形 四角形 特別な点 三角形 正多面体を作ってみよう ブック Bunryu Kamimura 天体シュミレーション ブック Bunryu Kamimura ピタゴラスの定理(三平方の定理)の証明 ブック Bunryu Kamimura 円錐曲線の性質と活用 ブック Bunryu Kamimura
今回の算数は平面図形の3週目で「平面図形の面積」。 4年の復習が多いように思えますが、娘には願ったり叶ったり。 ここでのポイントは、 三角形の高さを見つける練習、 面積の等しい三角形を探す練習、 です。 当たり前のことですが、三角形の面積を求めるには「底辺」と「高さ」が必図心距離=(断面積×図心位置までの距離)の合計÷全断面積 では、右図の図心を求めてみましょう。 図心を求めるための下準備をしましょう ①まず、計算しやすくするため3つの長方形に分割します。 ②分割した長方形の面積を求めます。 a=5m×2m=10㎡ b=2m×4m=8㎡ c=10m×2m=㎡ ③X軸平面図形の難問1(12日大豊山中) 図のように,1辺の長さが18cmの正方形ABCDと,角アが90 の直角二等辺三角形があります。このとき,三角形BEFの面積を求めなさい。 (印刷する場合は平面図形の難問1(12日大豊山中)PDFへ)
図形の面積の求め方のテクニック「1 分割する」 問題)上の図の四角形abcdの面積は何c㎡ですか? 四角形を三角形二つに分割して解きます。 三角形abdと三角形bcdになりますので、 =6+5 =11c㎡ 図形の面積の求め方のテクニック「2 余分なところを引く」平面図形1 円とおうぎ形 周の長さと面積 無料で使える中学学習プリント http//chugakumanabihirobanet/ 2 解答 1.円 対角線 cmの平面図形 中1 数学の基本問題 数字やグラフの問題が得意でも、図形はちょっと・・・という生徒が意外に多いです。 中には「図形は数学ではない」と豪語する生徒もいます。 図形の扱いが苦手でも慣れることで何とかなりますから、何度も練習して、図を描いて、理解していきましょう




なぜ 周の長さの比は 25を使うんですか 下の15cmは使わないんですか Clear
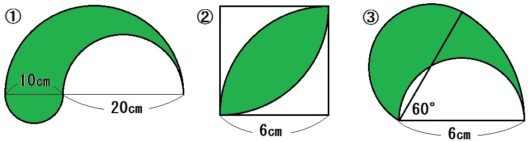



中学数学 平面図形 のコツ 円とおうぎ形
面積めんせき 面の広さ。 単位長さを1辺とする正方形の面積を単位として表す。 簡単な平面図形の面積は公式によって求められ,直線図形は三角形に分け,それらの面積の和をとる。 曲線で囲まれた平面図形や曲面の面積は一般に 積分 により計算§81 平面図形の面積 実数a とb とについて a ≤ b とし x y 0 a b y =f(x) y =g(x) x =a x =b 領域D ます.また,関数f とg とはa から b まで積分可能であり,区間a,b の各 実数x についてf(x)≤ g(x) とします. xy 座標平面において,連立不等式 a ≤ x ≤ b かつf(x) ≤ y ≤ g(x)本研究では、多種多様な図形の複雑さを分析するた め、形の情報をパラメータを使って示す。それは、周 囲長と頂点数である。周囲長は建築面積を100㎡ 建築平面図の図形的特徴に関する研究雑誌「新建築」における19年から08年の事例を対象として




平面図形をマスター 三角形の面積比 応用編その3




平面図形の面積 小5算数 偏差値45からの中学受験
よく出る図形100題 中学入試でよく出題される,あるいは差がつく問題ばかり100題を集めました。 がんばる受験生に役立つことを願って作成しています。 1ページ(の大きさ)に4題ずつ。切り分ければハガキ大の大きさになって,電車の中でもファミレスでお料理が来る前にでも,いつでも 平面図形① 四角形の面積公式の成り立ち そもそも面積とは何かというと広さのことを言います。算数によく出題される面積の単位は㎠(平方センチメートル)です。 1辺が1cmの正方形の面2h 2r 3r 3h 2h 2r 3r 3h Pの底面の半径を2rとするとQの底面の半径は3r Pの高さを2hとするとQの高さは3h ①表面積の比 Pの表面積 側面 2h×4πr=8πrh 底面 2r×2r×π×2=8πr2 よって 表面積 8πrh8πr2 =8πr (hr) Qの表面積 側面 3h×6πr=18πrh 底面 3r×3r×π×2=18πr2 よって 表面積
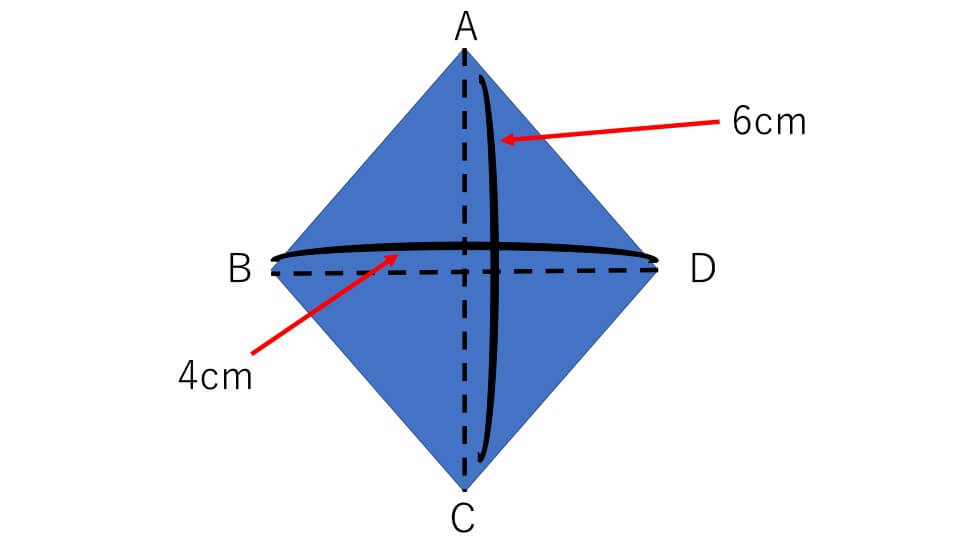



中学受験 算数 平面図形の面積 成り立ちから詳しく解説 中学受験アンサー




中学数学平面図形 公立高校入試の良難問 定期テストや高校入試に レオンの中学数学探検所
平面図形の苦手を解消! 三角形の面積比~基本編~ 算数に苦手意識があり、平面図形が特に苦手という人はまず基本の考え方から確認が必要です。 平面図形はある程度の基本パターンを学習していないと、「考えても解法の糸口がわからない」という状態になりやすいためです。 平面図形が解ける生徒が言う「ひらめいた! 」は「この問題、似たようなものを面積 (めんせき) とは、 線 (せん) で 囲 (かこ) まれた 平面 (へいめん) や 曲面 (きょくめん) の 広 (ひろ) さのことです。 このページでは、 様々 ( さまざま ) な 平面 ( へいめん ) 図形 ( ずけい ) の 面積 ( めんせき ) の 求 ( もと ) め 方 ( かた ) を 一覧 ( いちらん ) にまとめています。 算数「平面図形の面積と角度」中学受験 中学受験 問題6 右の図1の二等辺三角形を、図2のように3つおいたとき、アの角度は何度ですか。 (早稲田中 08年) <問題6の考え方と答え> まずは、次のように、図にA~Gまで点をつけました。 同じ二等辺




年度中学入試 平面図形の最難問 東大カリスマ塾長 浜田一志公式ブログ 9割が伸びる 文武両道 勉強法



無料 中1数学 基本問題 解答プリント 平面図形5 おうぎ形の弧と面積 138
ヘロンの公式の証明と使用例 ヘロンの公式とは,三角形の3辺の長さから面積を求めるための公式です。 3辺の長さが a, b, c a, b, c a,b,c の三角形の面積 S S S は, s = a b c 2 s=\dfrac {abc} {2} s = 2a b c図形1 図形の移動 作図1 作図2 作図3 作図4 作図5 おうぎ形 (半径と中心角から弧や面積を出す) おうぎ形 (半径と弧または面積から中心角を出す) おうぎ形 (半径を求める) おうぎ形 (総合) 平面図形面積 (発展) ① 70cm 2 ② 9πcm 2 ③ 56cm 2 ④ 11πcm 2 ⑤ (25π50)cm 2 ① 47 2 πcm 2 ② 33 5 πcm 2 ③ (8π16)cm 2 (1) 15πcm 2 (2) 216° (1) 6πcm (2) 135° (1) 18cm (2) 50°A = 面積 P = 円周(近似式) 円錐 V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径



平面図形の難問1 日大豊山中




中学受験 算数 平面図形の面積 成り立ちから詳しく解説 中学受験アンサー
面積の比はその共通角をはさむ2辺の積、 三角形abcの面積:三角形adeの面積=5×9:2×4=45:8 で求められるというものです。 この解き方を習っている場合は、 ア×3:イ×2=2:1 なので ア×3:イ×2=4:2=12:6 または「内項の積=外項の積」を利用して 平面図形「30度(あるいは150度)をはさむ辺×辺÷4でその三角形の面積」 面積計算は "たて×よこ" を基礎にしています。というより、面積はそのように定義されている、といったほうが正確かもしれません。平面図形 ・ 直線や平面の位置関係 ・ 扇形の弧の長さと面積,柱体や錐体 及び球の表面積・体積 ・ 空間図形の構成と平面上の表現 (見取図,展開図,投影図) 空間図形 ・ 関数関係の意味 ・ 比例,反比例の意味 ・ 座標の意味 ・ 比例,反比例の特徴 ・ 比例,反比例を用いること 比例,反



面積 これが中学入試に出た図形問題




つまずきをなくす 小4 5 6 算数 平面図形 Amazon Com Books
平面図形 ア 基本的な作図とその活用 「図形」は、「数と式」「関数」「資料の活用」と比較して、 ウ 図形の面積 おさらいとなります ① 平行四辺形系の面積 長方形の面積 = (底辺)×(高さ) でしたね 大前提の 1×1 ですね 単位は、 cm なら 1 cm 2 、 m なら 1 m 2 、 μ m (マイクロメーター 面積が S S S であるような三次元空間内の平面図形を y z yz yz 平面に正射影した図形の面積を S x S_x S x とおく。同様に S y, S z S_y,S_z S y , S z も定義する。このとき S 2 = S x 2 S y 2 S z 2 S^2=S_x^2S_y^2S_z^2 S 2 = S x 2 S y 2 S z 2平面図形の幾何学と歴史 山岡 緑 になるが、面積と長さを加えたり、面積と体積を加えたりす ることは意味がないものとして固く禁じられていた。 デカルトによって可能になった表現法を使うと、x2=ax+b2 のように次元を揃えなければならなかったものが、 y=x3+ax2+bx+cのように



灘中学 07年 平成19年度 平面図形の面積 灘中学の算数に挑戦 まいにち一題 中学受験問題研究 灘分校




四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ
「第512回 女子中の平面図形 2」 近年の女子中入試の中から、「平面図形」の問題を見ています。 前回は「角の大きさ」に関する1行問題をご紹介しましたが、今回は 「求積(面積を求める)」 の問題について考えていこうと思います。 問題は、面積の公式と「解法知識」を使って解くもの314×81= 正方形や円などの面積を速く正確に計算するために、同じ数をかけた積(二乗・自乗)の計算方法をマスターしましょう。 (参考) → 二乗の速算法 平面図形の面積の基本問題 問題1 次の図形の黒くぬった部分の面積を求めなさい。 → 解答 問題2辺の比と面積(平面図形) <辺の比と面積(平面図形)の問題> (1)(図1)で,ADDB = 1 1, BEEC=21, CFFA=53です。 三角形DEFの面積と三角形ABCの面積の比を求めなさい。 (2)(図2)の三角形ABCで,BD:DC=3:2, AE:EC =2:1です。 AF FB を求めなさい。
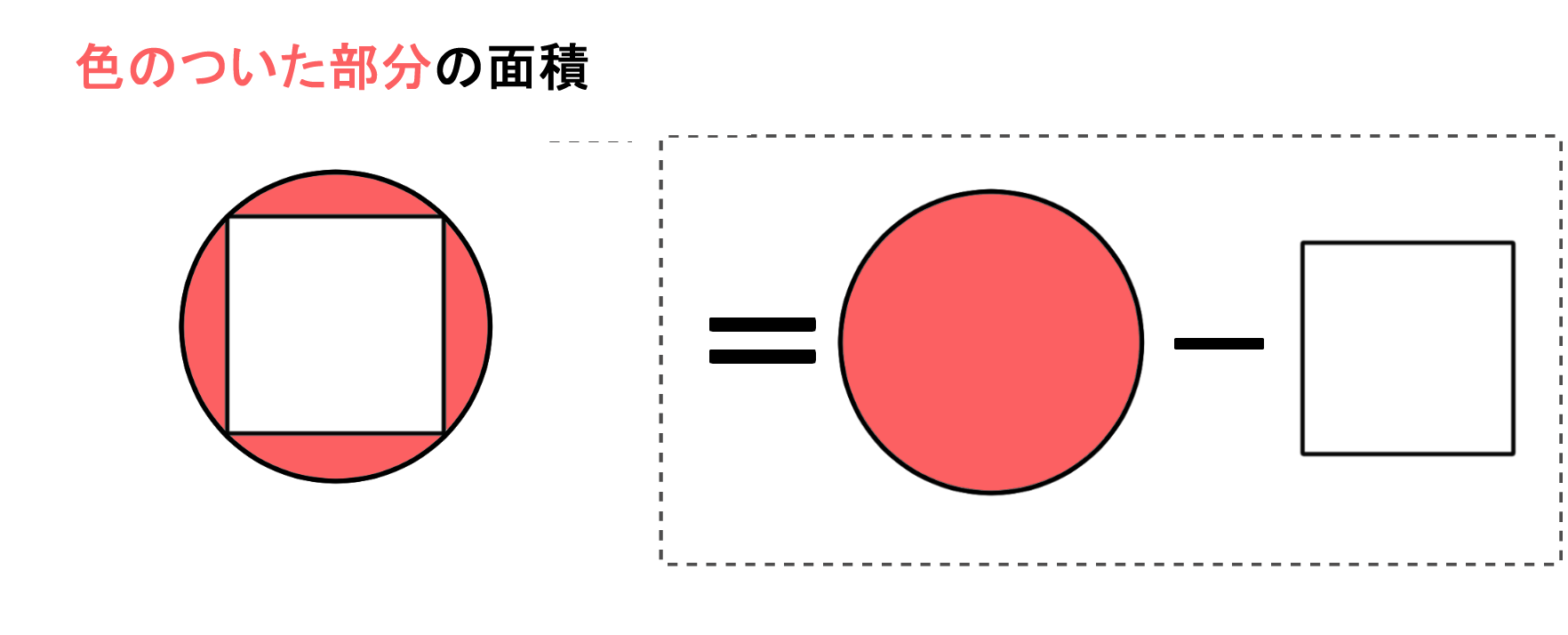



色のついた部分のへんな形の図形の面積を求める問題 バカでもわかる 中学数学




六甲学院中2018年 平面図形ー 中学受験算数の良問 難問 基本問題
平行四辺形の面積=底辺×高さ ひし形の面積=対角線×対角線÷2 台形の面積= (上底+下底)×高さ÷2 三角形の面積=底辺×高さ÷2 円の面積=半径×半径×円周率 (314) おうぎ形の面積=半径×半径×円周率×中心角/360° 公式の成り立ちから知りたい人や公式がまだ曖昧な人は こちらの記事 を読んでから、これから解説する問題に取り組んでください。 中学




平面図形の面積2週目 小5算数 偏差値45からの中学受験
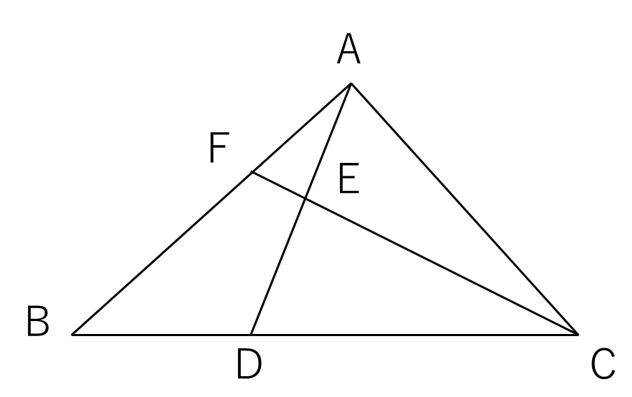



三角形の面積比をてんびんで解く 中学受験プロ講師ブログ




算数苦手さん向けの 平面図形 円の面積 間違いポイントと対策 新小5 サピックス 中学受験 知識ゼロから合格へ



平面図形の面積 復習問題として平面図形のプリントを出され Yahoo 知恵袋




なぜ 周の長さの比は 25を使うんですか 下の15cmは使わないんですか Clear




面積の求め方 算数の教え上手 学びの場 Com




正方形と扇形の面積をつかった問題がわかる3ステップ Qikeru 学びを楽しくわかりやすく
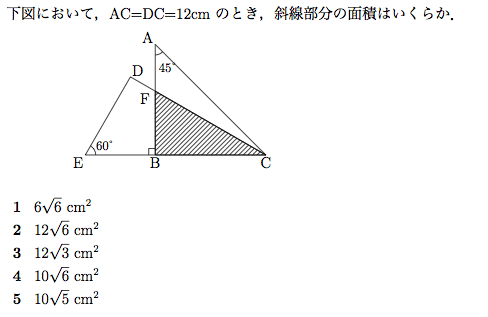



平面図形 面積 知能問題 数的処理 判断推理 数的推理 数学パズル spi 空間把握 解いてみてください



中1数学 発展 応用問題プリント 平面図形のおうぎ形の弧と面積 138
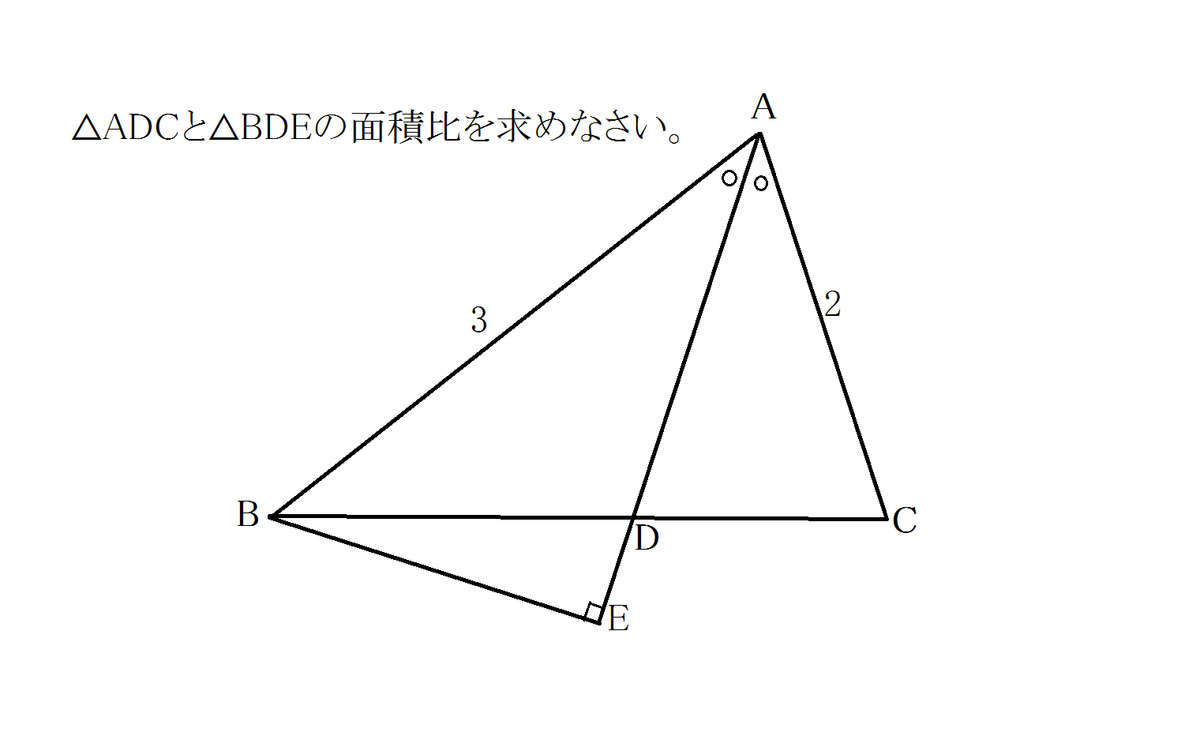



中学数学発展 シンプルだけど難しい ラ サールの難問 平面図形 定期テストや高校入試に レオンの中学数学探検所



灘中学 08年 平成年度 平面図形の面積 灘中学の算数に挑戦 まいにち一題 中学受験問題研究 灘分校




東大寺中2017年 平面図形ー 中学受験算数の良問 難問 基本問題
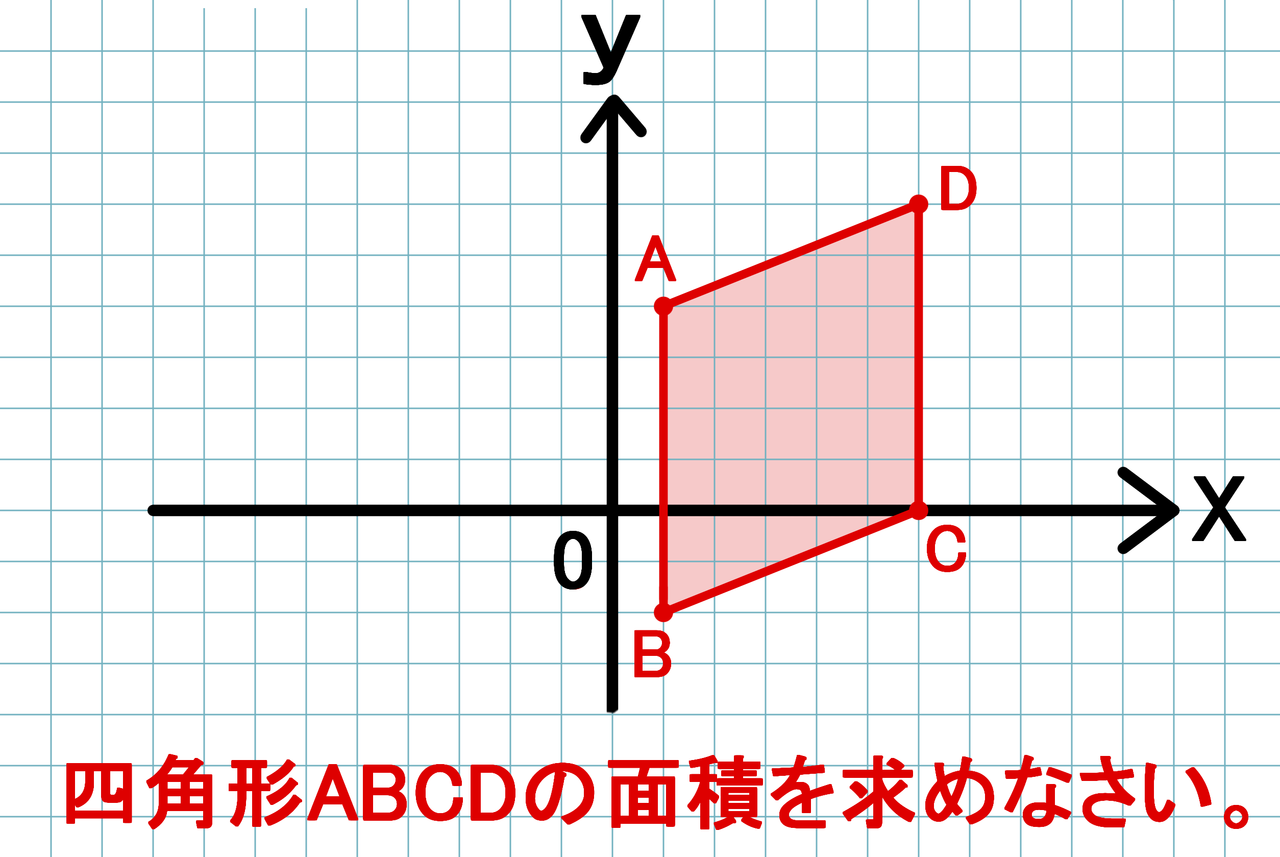



座標平面に描かれた図形に関する問題 バカでもわかる 中学数学




円とおうぎ形 応用 無料で使える中学学習プリント
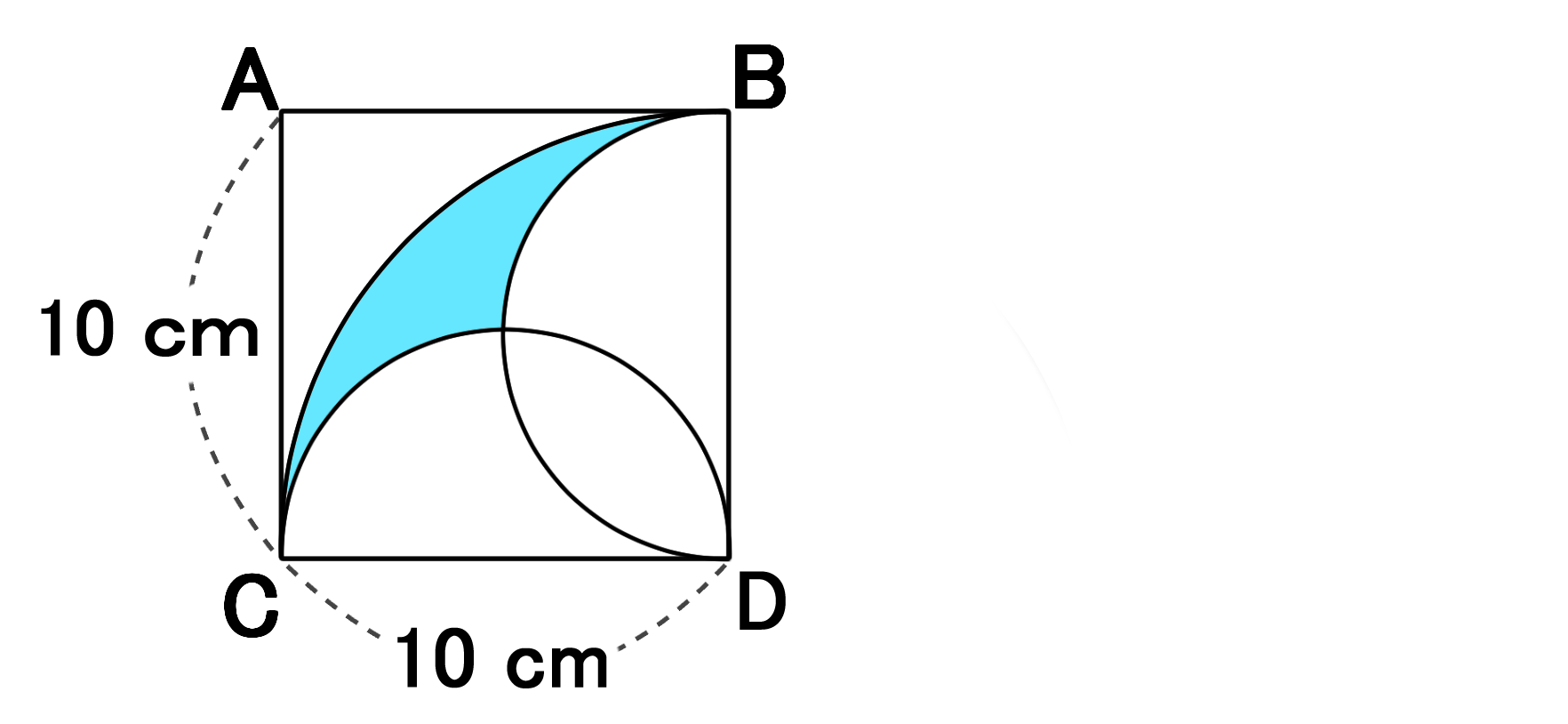



色のついた部分のへんな形の図形の面積を求める問題 バカでもわかる 中学数学




ボード 子供の教育 のピン



面積の求め方 算数の教え上手 学びの場 Com




面積の求め方 算数の教え上手 学びの場 Com




第30回 平面図形 複合図形の求積 5年生 日能研の歩き方




中学受験の平面図形をマスター 三角形の面積比 応用編その1



1




面白い算数問題 中学受験 中学入試 算数 解説 平面図形 面積 Youtube




豊島岡女子中 算数の図形問題 プロが教える重要ポイント




第9回 平面図形 長方形 正方形の面積 4年生 日能研の歩き方




いろいろな面積を求める問題1 中学受験準備のための学習ドリル




2 2 8cm 6 Cm Lihat Cara Penyelesaian Di Qanda
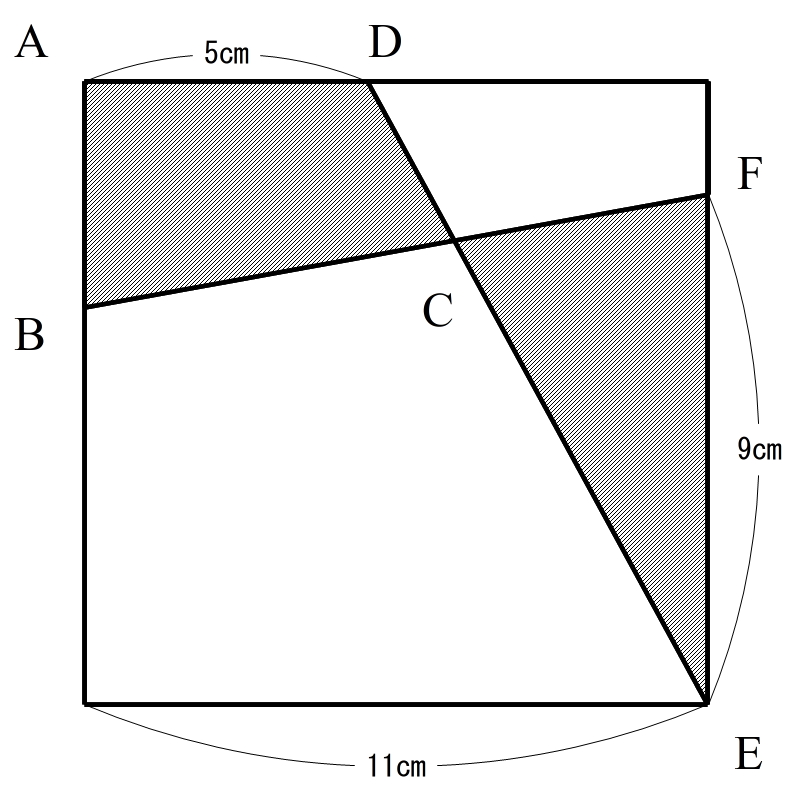



等積な平面図形 女子学院中 14 中学受験入試標準問題集 今日の1問




高校数学b 三角形の面積のベクトル表示 成分表示とその証明 受験の月
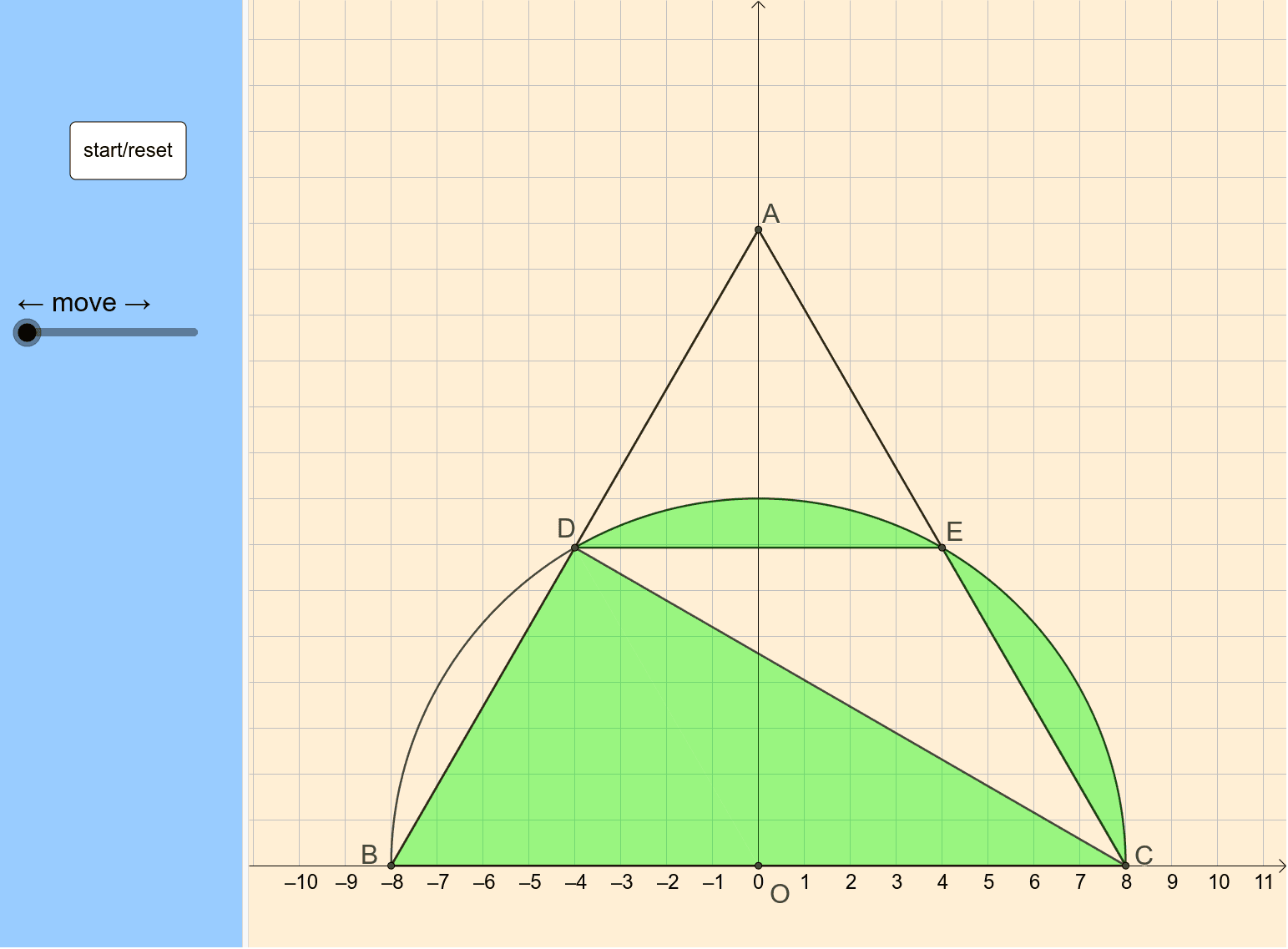



平面図形 円とおうぎ形の面積 Geogebra




この図形の面積の求め方を教えてくださいm M Clear




平面図形をマスター 三角形の面積比 応用編その2




平面図形をマスター 三角形の面積比 応用編その3




中学受験 算数 平面図形の面積 成り立ちから詳しく解説 中学受験アンサー



平面図形の面積 学ぶ 教える com



平面図形 算数解法の極意



無料 中1数学 テスト対策問題 問題プリント 127 平面図形3 実力アップ
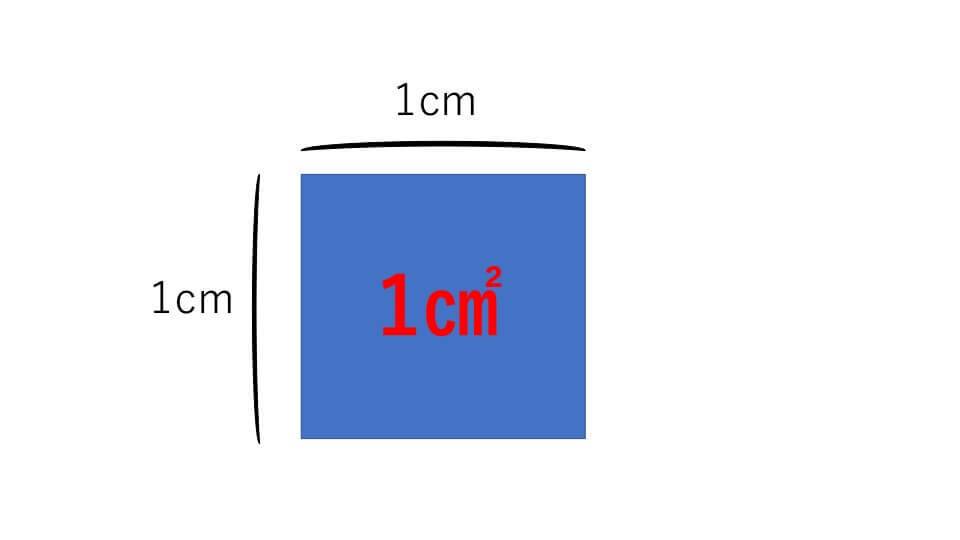



中学受験 算数 平面図形の面積 成り立ちから詳しく解説 中学受験アンサー



1
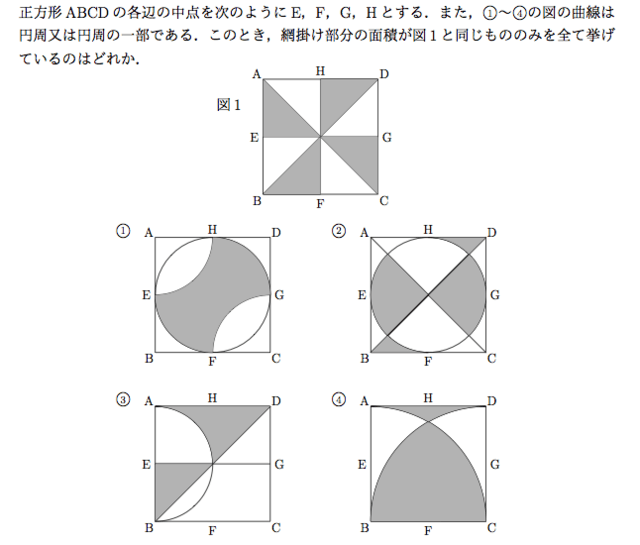



面積移動 知能問題 数的処理 判断推理 数的推理 数学パズル spi 空間把握 解いてみてください




平面図形の面積 まとめ7 8 いろいろな図形の面積 Youtube



帝京大学中10 2 の 6 平面図形 複雑な図形の面積を2等分する 気まぐれ解説カフェ 仮



1




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ




高校数学 座標平面上の三角形の面積の公式 受験の月




算数 平面図形 面積の問題 まいにち一題 中学受験過去問題研究




平面図形をマスター 三角形の面積比 応用編その2




円とおうぎ形 いろいろな面積の問題 中学受験準備のための学習ドリル




平面図形の面積 第105問 洛南高校附属中学 受験問題 年 令和2年度 算数 まいにち一題 中学受験過去問題研究
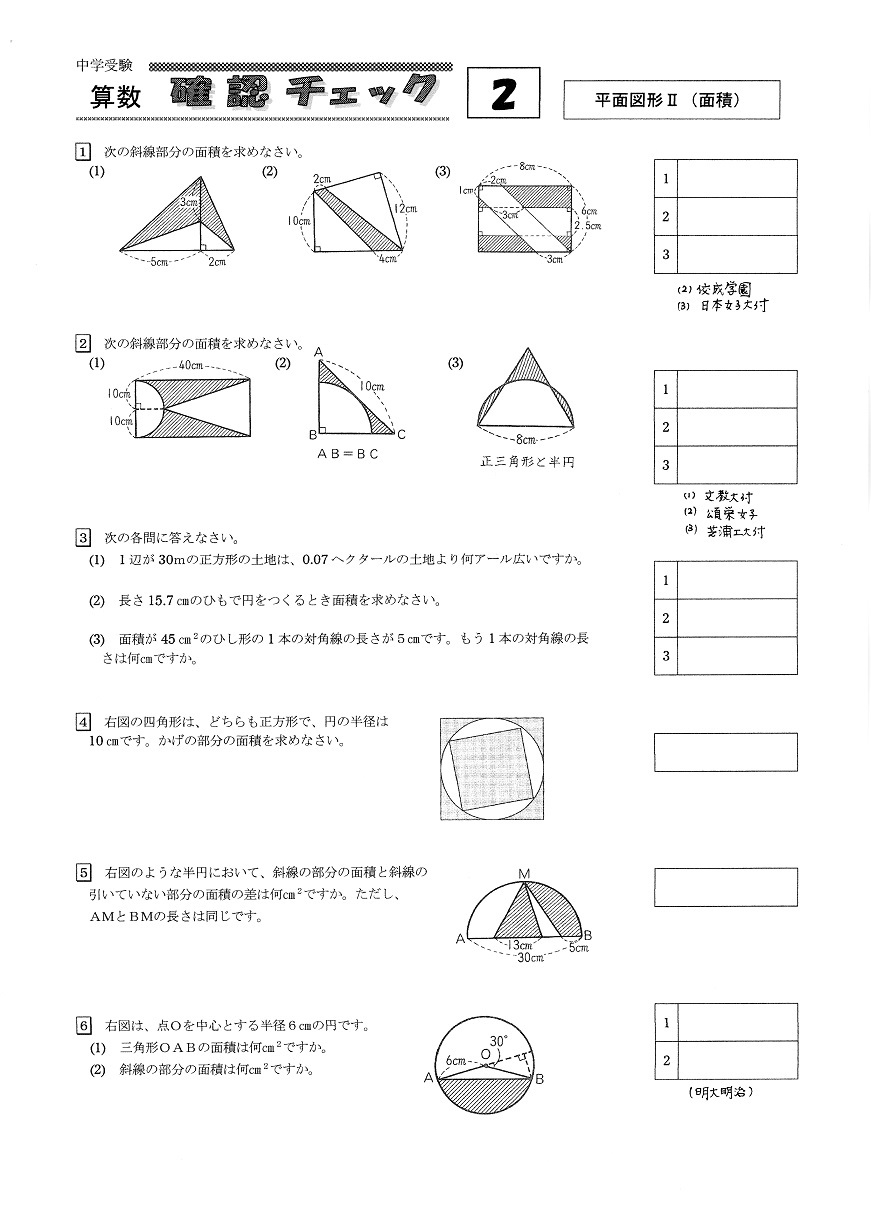



中学受験 算数確認チェック2 平面図形 面積 グランパは元塾長




標準 おうぎ形と正方形の面積 なかけんの数学ノート




高校数学 平面図形の回転体の体積 受験の月
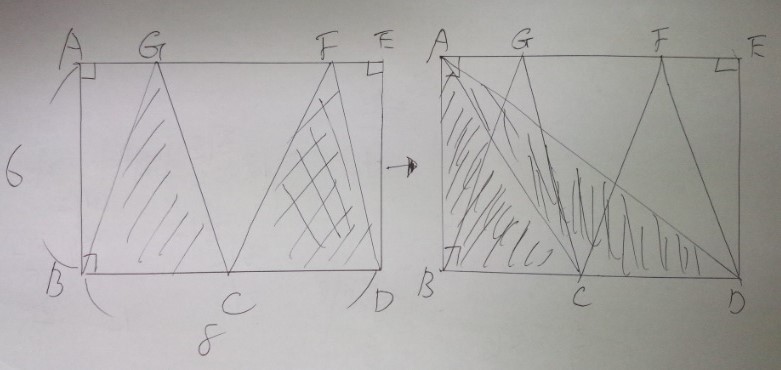



図形の面積の求め方のテクニック 基本編 中学受験 塾なし




平面図形 面積比 和洋九段女子中 2018年 算数 数学 受験 算太 数子の算数教室 う山先生 の はてなブログ




平面図形が苦手な人は必見 三角形の面積比と辺の比の関係 基礎編
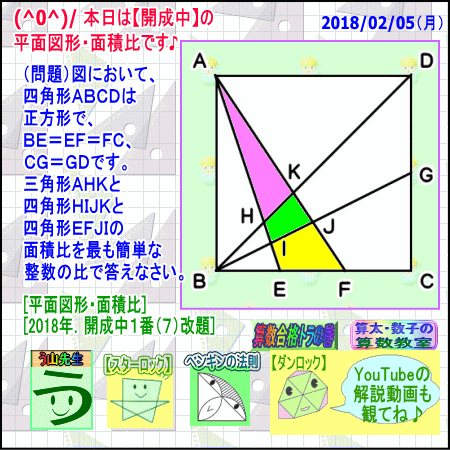



平面図形 面積比 開成中2018年 算数 数学 受験 算太数子 中学受験 算数プロ家庭教師 算数合格トラの巻 エキサイト ブログ



平面図形の面積 第68問 奈良学園中学 1998年 照曜館中学 09年 入試問題 算数 まいにち一題 中学受験過去問題研究




数学 面積比と線分比をシッカリわかると チェバの定理を深く理解できるよ 平面図形 中学数学 高校数学 行間 ぎょうのあいだ 先生




平面図形と面積 比を究める15題 Myisbn デザインエッグ社 清水良太郎 本 通販 Amazon
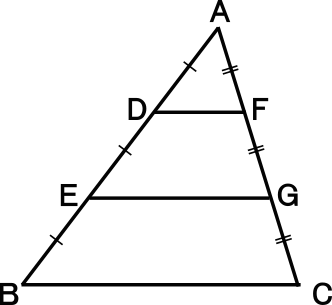



中学3年数学練習問題 相似な平面図形の面積の比 図形と相似




面白い算数問題 中学受験 中学入試 算数 解説 平面図形 面積 Youtube




面積比の公式まとめ 相似比と面積比と体積比の関係もあわせて解説 遊ぶ数学




中学受験算数 平面図形編 Flashcards Quizlet
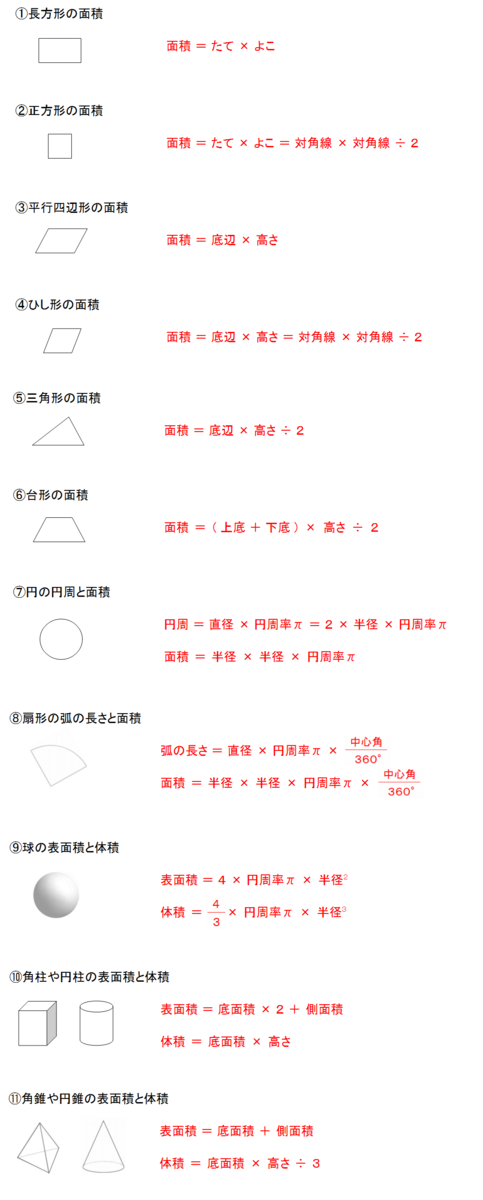



図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師
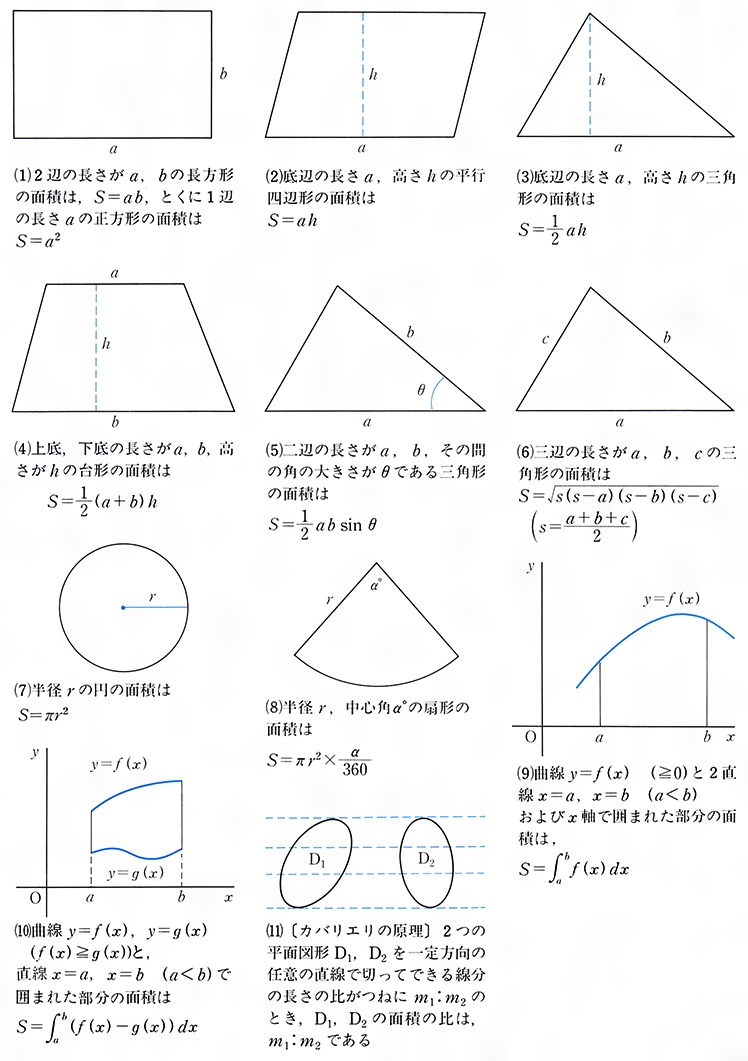



面積とは コトバンク




平面図形の面積比 数学i フリー教材開発コミュニティ Ftext
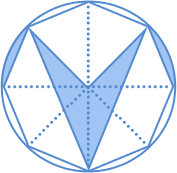



算数 平面図形の面積と角度 中学受験 ベネッセ教育情報サイト




円の面積 練習応用 Youtube



数学 中3 64 三平方 平面図形への利用 面積編 Youtube
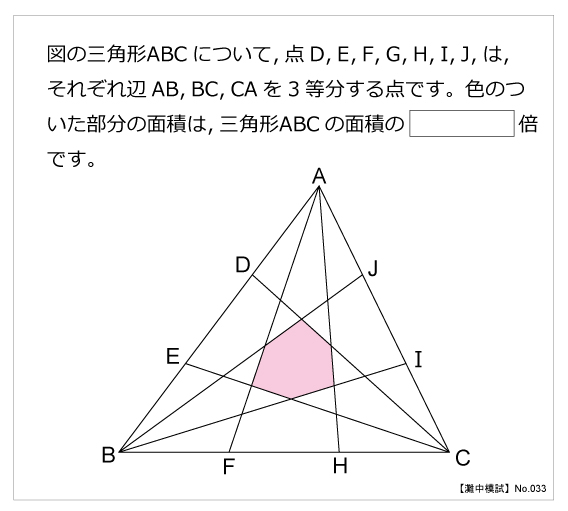



灘中模試 No 033 平面図形 算数星人のweb問題集 中学受験算数の問題に挑戦




つまずきをなくす小4 5 6算数平面図形 角度 面積 作図 単位 通販 セブンネットショッピング



図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師




中学3年の三平方の定理と平面図形です この問題の台形の面積を求めてください Clear



平面図形の面積 灘 2007 どう解く 中学受験算数




辺の比と面積 平面図形 中学受験の算数 理科ヘクトパスカル




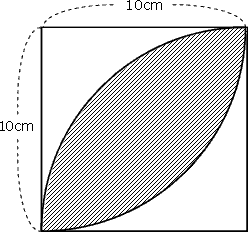
はっぱ型 の図形の面積 身勝手な主張
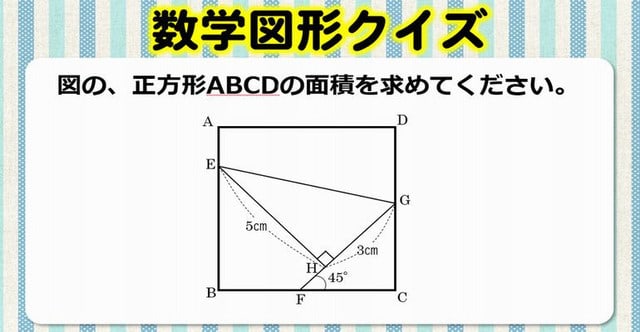



数学図形クイズ シンプルだけどひらめきが必要な正方形の面積の良問 暇つぶしに動画で脳トレ



算数 テーマ別 ポイント集 平面図形 10 14 中学受験の勉強法 偏差値アップの学習法



算数 テーマ別 ポイント集 平面図形 10 14 中学受験の勉強法 偏差値アップの学習法




中1 数学 中1 77 おうぎ形の弧と面積 ややこしい図形編 Youtube
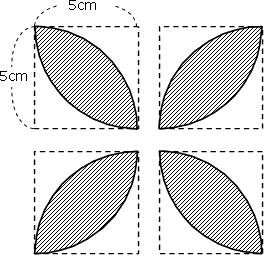



面積の求め方 算数の教え上手 学びの場 Com



3



算数 テーマ別 ポイント集 平面図形 10 14 中学受験の勉強法 偏差値アップの学習法




図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト




平面図形 面積比 和洋九段女子中改題 2018年 算数 数学 受験 中学受験 算数プロ家庭教師 算太 数子の算数教室 goo ブログ
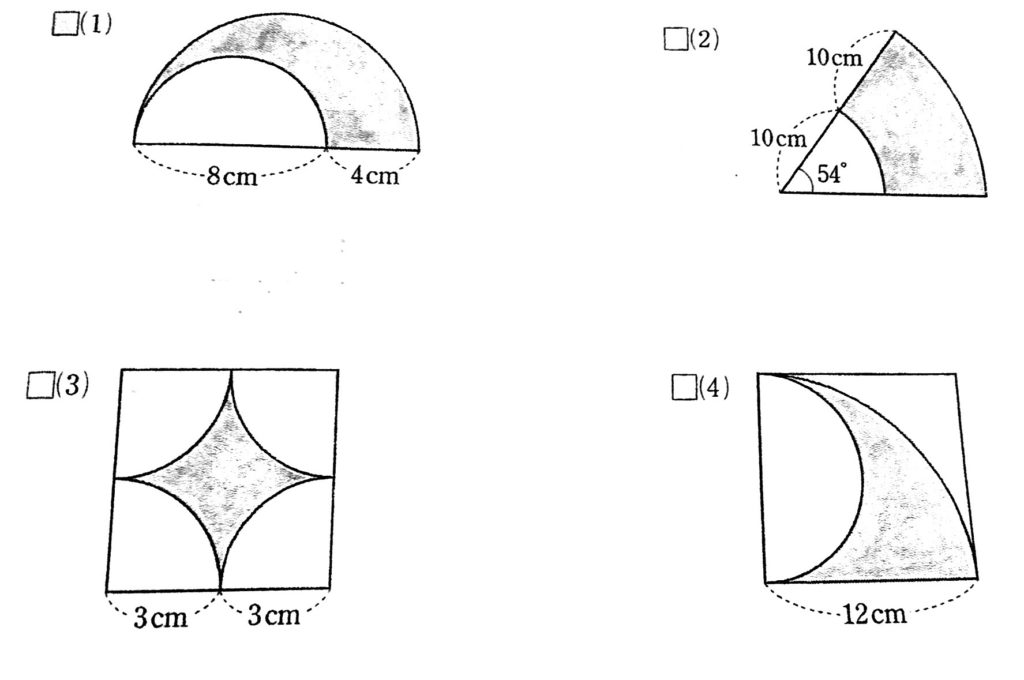



おうぎ形の応用 影の部分の面積 周の長さの求め方 数スタ




辺の比 面積比 相似 16年東京都 高校入試 数学 良問 難問




平面図形をマスター 三角形の面積比 応用編その2




平面図形の面積の求め方 基本編 中学受験 塾なし の



0 件のコメント:
コメントを投稿